SIMULATION OF A SIGNALIZED INTERSECTION:
A Resource for Undergraduate Students of Statistics

Overview:

VIEW SIMULATION

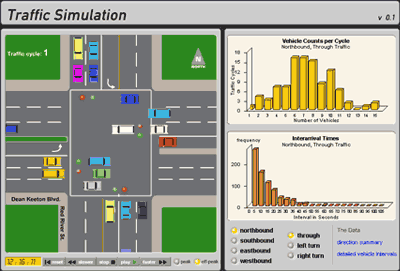
A signalized intersection offers a wealth of data. From vehicle counts, speeds and occupancies to driver and passenger characteristics, the possibilities are almost endless. A simulation and statistical analysis can illustrate and simplify this seemingly complex process.

While a variety of intersection data exists, at this site, you can observe assembly and evaluation of two key sets of intersection data for each of the twelve movements: inter-arrival times between vehicles and counts of vehicles per cycle. A movement describes vehicle approach direction (northbound, southbound, westbound, and eastbound) and final maneuver (through, right turn, and left turn). A cycle is the series of green (and red) phases that completes one full use of the intersection (so that every movement is served, exactly once in most signal timing plans).

The simulations are based on data acquired at the intersection of Red River Road and Dean Keeton Street just west of IH 35 on the northeast corner of the University of Texas at Austin campus. Very little data acquisition is required for this sort of simulation. Necessary inputs are:

1. estimates of average arrival rates (vehicles per minute) for each movement
2. distributional assumptions for the arrival process (Poisson counts, or exponentially distributed inter-arrival times, were assumed here)
3. signal “logic” (the signal’s timing is fixed here)
4. intersection geometry (such as the number of through and left-turn lanes in each approach).

The estimates of arrival times came from a period of just two hours: one during a weekday morning (“rush hour” or “peak period”), the other during a weekday lunch hour (“off-peak period”). The total cycle lengths at those two times of day are 100 and 140 seconds, respectively.

Instructional Objectives:

By reviewing the simulation, you will be able to do the following:

• Identify a number of measurable variables that arise at an intersection.
• Review histograms for both continuous and discrete random variables.
• Describe the connection between Poisson and exponential distributions.

Key Concepts & Questions:

After you have looked at the simulation, try to answer the following questions.

1. Data surrounds us. Name at least five variables (other than vehicle counts and inter-arrival times) that may be observed at a signalized intersection. Determine which are discrete and which are continuous in nature.
2. Complexity can arise from simplicity. What four types of information were required for this intersection’s simulations?
3. What does assumption of the Poisson distribution for vehicle counts (or exponential for interarrival times) imply about the arrival process? Under what settings would this assumption fail to describe a real arrival process at an intersection?
4. The sum of independent Poisson variables is a Poisson random variable. What distribution does the total count histogram follow and why?

Answers

 

Key Quantitative Questions:

After downloading the appropriate data set(s), answer the following questions.

1. Using the original data, what is the average arrival rate of vehicles in the NBTH direction (in vehs/minute)?
2. What is the probability that exactly 5 vehicles arrive in the NBTH direction during a single peak-period phase?
3. What is the probability that more than 10 seconds elapse between successive vehicles arriving in the NBTH direction?
4. How many vehicles should the NBLT bay be designed to accommodate so that it holds 95% of all left-turning queues that are likely to develop during the peak period? (Note: You may consider only vehicles arriving during this movement's red period.)

Development:

This site was envisioned by Dr. Kara Kockelman, Associate Professor of Civil Engineering, at the University of Texas at Austin, and coded in Flash software by the College of Engineering’s Faculty Innovation Center’s Matt Mangum and Amar Mabbu, with assistance from Dr. Kathy Schmidt. Graduate students Chris Frazier and Qi Wang contributed all data. Special thanks to David Castillo at www.flashsim.com.