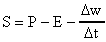 (1)
(1)Seann M. Reed
This document summarizes the soil-water budget methodology as applied to a study of the water resources of the Niger River basin. This work is part of the FAO/UNESCO Water Balance of Africa project.
Basin-averaged values of "surplus" water were estimated for 167 sub-basins of the Niger River basin for two scenarios: long term average climatic conditions and conditions during a historical period (short term) representative of dry conditions, July 1983 to Dec. 1990. The phrases long term and short term will be used throughout the remainder of this document to refer to these two cases. Surplus is water which does not evaporate or remain in soil storage and includes both surface and sub-surface runoff.
Part I of this report to FAO/UNESCO describes the methodolgy and results for soil-water budgeting. Part II provides a technical description of how computations were made and includes a list of files and programs and there locations on the project CD-ROM. Part II has not been converted to HTML and has not been placed on our HTTP server because the tedious details are not expected to be of general interest (contact the author if you would like more details). A budgeting exercise created for the GIS in Water Resources class is available for those who wish to see how the calculations work.
Despite numerous uncertainties associated with simple soil-water budget model like the one used in this study, many researchers have applied this type of model to problems ranging from catchment scale studies to the global water balance and climate change scenerios (Thornthwaite, 1948; Budyko, 1956; Manabe, 1969; Mather, 1978; Alley, 1984; Willmott et al., 1985; Mintz and Walker, 1993; Mintz and Serafini, 1992). The popularity of this approach in hydrologic studies is most likely due to its simplicity. The simple bucket model used here requires minimal input data : precipitation, temperature, net-radiation, and soil-water holding capacity. For catchment scale applications, the soil-water budget approach for predicting runoff has shown reasonable agreement with measured annual flows, but has not shown good agreement with monthly flows (Mather, 1978). Although the soil-water budget roughly accounts for the soil storage effects on the time distribution of surface and sub-surface runoff, it has not demonstrated accurate prediction of monthly flow volumes.
For the Niger Basin project, a surface water routing model takes computed surplus as input and optimizes overland flow and streamflow loss parameters to predict monthly flows. For more information about the surface water routing model, link to Ye's Map-based Surface Water Modeling page.
Three difficult questions involved with simple soil-water
budget calculations that are discussed to in this document are
how to deal with situations when inadequate daily data are available
and only monthly data can be used, how to derive spatially distributed
estimates of climatic variables from point calculations, and how
to estimate potential evaporation. Section IIc discusses time
stepping (daily vs. monthly). Section V describes an approach
for generating climate surfaces from point data and explores the
sensitivity of water surplus calculations to two methods of estimating
potential evaporation. Sections I-IV provide background material
and a detailed description of the soil-water budget methodology.
Sections VI briefly describes results.
Where detailed data about soil layers, depth to groundwater,
and vegetation are not available, hydrologists have often resorted
to simple bucket models and budgeting schemes to model near-surface
hydrology. The soil-water budget is a simple accounting scheme
used to predict soil-water storage, evaporation, and water surplus.
A typical budgeting time step is one day. Surplus is the fraction
of precipitation that exceeds potential evapotranspiration and
is not stored in the soil. The simple model used here does not
distinguish between surface and subsurface runoff, so surplus
includes both. For the Niger project, the main purpose of calculating
the water budget is to estimate surplus, which serves as input
to groundwater and surface water flow models. With this in mind,
the basic equation for calculating surplus is:
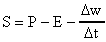
In Equation 1, S is surplus, P is precipitation, E is evaporation, w is soil moisture, and t is time. Horizontal motion of water on the land surface or in the soil is not considered by this model. Snow melt was ignored in the water budget computations for this study because temperatures throughout the study region remain above freezing throughout the year.
A major source of uncertainty in evaluating Equation
1 is estimating the evaporation. Estimation of evaporation is
based upon knowledge of the potential evapotranspiration, available
water-holding capacity of the soil, and a moisture extraction
function. The concepts of water-holding capacity and the method
for evaluating Equation 1 are discussed here, followed by a more
detailed discussion of the potential evapotranspiration concept
in Section III.
In order to calculate the soil-water budget, an estimate
of the soil's ability to store water is required. Several terms
are used by soil scientists to define the water storage capacities
of soils under different conditions. The field capacity or drained
upper limit is defined as the water content of a soil that has
reached equilibrium with gravity after several days of drainage.
The field capacity is a function of soil texture and organic content.
The permanent wilting point or lower limit of available water
is defined as the water content at which plants can no longer
extract a health sustaining quantity of water from the soil and
begin to wilt. Typical suction values associated with the field
capacity and wilting point are -10 kPa (-0.1 bars) and -1500 kPa
(-15 bars) respectively. Like water content, field capacity and
permanent wilting point are defined on a volume of water per volume
of soil basis. Given these two definitions, the water available
for evapotranspiration after drainage ( or the available water-holding
capacity ) is defined as the field capacity minus the permanent
wilting point. Table 1 gives some typical values for available
water-holding capacity.
Table 1: Water Retention Properties for Agricultural Soils
(Values Taken from ASCE,1990, Table 2.6, p. 21.)
| Texture Class | Field Capacity | Wilting Point | Available Capacity |
| Sand | 0.12 | 0.04 | 0.08 |
| Loamy Sand | 0.14 | 0.06 | 0.08 |
| Sandy Loam | 0.23 | 0.10 | 0.13 |
| Loam | 0.26 | 0.12 | 0.15 |
| Silt Loam | 0.30 | 0.15 | 0.15 |
| Silt | 0.32 | 0.15 | 0.17 |
| Silty Clay Loam | 0.34 | 0.19 | 0.15 |
| Silty Clay | 0.36 | 0.21 | 0.15 |
| Clay | 0.36 | 0.21 | 0.15 |
For budgeting calculations, it is useful to know
the total available water-holding capacity in a soil profile.
This value is typically expressed in mm and can be obtained by
integrating the available water-holding capacity over the effective
depth of the soil layer. A one meter soil layer with a uniform
available water-holding capacity of 0.15 has a total available
water-holding capacity of 150 mm. For the remainder of this paper,
the term water-holding capacity means total available water-holding
capacity in units of mm. Soil-water storage (mm) is denoted by
w and water-holding capacity is denoted with w*. A large water-holding
capacity implies a large annual evapotranspiration and small annual
runoff relative to a small water-holding capacity under the same
climatic conditions.
To estimate the actual evapotranspiration in the
soil-water budget method many investigators have used a soil-moisture
extraction function or coefficient of evapotranspiration beta
which relates the actual rate of evapotranspiration to the potential
rate of evapotranspiration based on some function of the current
soil moisture content and moisture retention properties of the
soil.
E = beta * PE
(2)
Dyck, 1983, Table 1, (reprinted in Shuttleworth, 1993, Table 4.4.6)
provides a summary of some moisture extraction functions used
by different investigators. Mintz and Walker, 1993, Figure 5,
also illustrates several moisture extraction functions. Many researchers
agree that soils show the general pattern of behavior that moisture
is extracted from the soil at the potential rate until some critical
moisture content is reached when evapotranspiration is not longer
controlled by meteorological conditions. Below this critical point,
there is a linear decline in soil moisture extraction until the
wilting point is reached. This type of behavior is illustrated
by Shuttleworth, 1993, Figure 4.4.3 p. 4.46 and Dingman, 1994,
Figure 7-21. Shuttleworth, 1993, notes that the critical moisture
content divided by the field capacity is typically between 0.5
and 0.8. The type of moisture extraction function just described
is commonly applied to daily potential evaporation values. A simpler
function, beta
= w/w*, has been applied to monthly values.
There are several drawbacks to using simple soil
moisture extraction functions. Mintz and Walker, 1993, cite field
studies that show beta
may vary with potential evapotranspiration for a given soil wetness
and beta may
also vary with leaf-area index. In addition, the spatial variation
of water-holding capacity is difficult to determine. A new and
possibly better approach to determining the relationship between
plant transpiration and potential evapotranspiration is to correlate
beta with satellite-derived
indices of vegetation activity so that beta will reflect plant growth stage and the spatial
vegetation patterns. Gutman and Rukhovetz, 1996, investigate this
possibility. Their approach still requires an estimate of potential
evapotranspiration.
Soil-water budget calculations are commonly made
using monthly or daily rainfall totals because of the way data
are recorded. Computing the water balance on a monthly basis involves
the unrealistic assumption that rain falls at constant low intensity
throughout the month, and consequently surplus estimates made
using monthly values are typically lower than those made using
daily values. Particularly in dry locations, the mean potential
evaporation for a given month may be higer than the mean precipitation,
yet there is observed runoff, and budgeting with monthly values
may yield zero surplus. For this reason, the use of daily values
is preferred over monthly values when feasible. In this study,
daily rainfall records were provided by FAO for a number of stations
in the Niger basin; however, the spatial coverage of these stations
is sparse in some areas, and it is difficult to interpolate daily
rainfall over space.
Because of the difficulty in estimating daily rainfall
at our regularly spaced computational points, and because a consistent
basis for comparison is needed between the short term case (for
which daily data are available) and the long term case (only monthly
data are available), monthly data were used in this study. However,
the use of monthly data does not yield enough surplus to match
observed river flows in some areas of the Niger basin even with
the assumption of zero overland flow and stream losses. To resolve
this problem, a modification was made to the commonly used bucket
model in which it is typically assumed that no surplus is generated
until the soil is completely saturated with water; this assumption
is not consistent with situations where the rainfall rate exceeds
the infiltration rate of the soil. In our modified model, a fraction
of the precipitation is extracted and declared runoff, before
remaining precipitation is passed to the soil. This extraction
of precipitation is represented by the P*alpha
term in Equation 3 below. This scheme generates more runoff, enough
to satisfy mass balance constraints in most areas of the Niger
basin. Without this term, the model will predict zero runoff during
many months of the year when some observed streamflow actually
occurs. The runoff extraction term roughly accounts for "event"
or "quick" flow that cannot be modeled using monthly
averaged values.
Equation 3 describes how soil moisture storage is
computed.
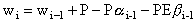
In Equation 3, w(i) is the current soil moisture, w(i-1)
is the soil moisture in the previous time step, P is precipitation,
PE is potential evaporation, alpha
is the runoff extraction function, and beta
is the soil-moisture extraction function. With monthly data, computations
are made on a quasi-daily basis by assuming that precipitation
and potential evapotranspiration for a given day are equal to
their respective monthly values divided by the number of days
in the current month. Several conditions apply when evaluating
Equation 3: If w(i) drops below zero, then set w(i)
equal to 0.01; if w(i)>w* where w* is the water-holding
capacity, then the surplus for that day is w(i)-w*+P*alpha.
The soil-moisture extraction function beta=w/w*
was used for this study. Since there is no precedent for the use
of a runoff extraction function (alpha),
the formulation of this function was more speculative and deserves
further study. In the mean time, a simple relationship, alpha
= w/w*, was used and yielded enough surplus to satisfy mass balance
constraints in the surface flow routing model.
If the initial soil moisture is unknown, which is
typically the case, a balancing routine is used to force the net
change in soil moisture from the beginning to the end of a specified
balancing period (N time steps) to zero. To do this, the initial
soil moisture is set to the water-holding capacity and budget
calculations are made up to the time period (N+1). The initial
soil moisture at time 1 (w(1)) is then set equal to the
soil moisture at time N+1 (w(N+1)) and the budget is
re-computed until the difference (w(1) - w(N+1))
is less than a specified tolerance.
The soil-water budget is most easily applied at single
points in space dictated by the location of climate stations where
water-holding capacity can be measured or estimated, but the result
of these point calculations must be interpolated over space in
order to get a surplus volume. An alternative approach taken in
this study was to use pre-computed climate, net radiation, and
water-holding capacity grids, augmented with climate station measurements,
to calculate the soil-water budget at each point on a 0.5 by 0.5
grid. Using a single value for precipitation, temperature, and
net radiation in each 0.5 cell seems reasonable at the monthly
time scale. The water-holding capacity may vary considerably within
each 0.5 cell, and the value used in budgeting calculations is
only an average property of the cell.
One aspect of the soil-water budget that involves
significant uncertainty and ambiguity is estimating potential
evapotranspiration. Just the concept of potential evapotranspiration
is ambiguous by itself, as discussed in the next section. Due
to limited meteorological data, two simple methods for estimating
potential evapotranspiration were considered for the Niger basin
study, the Priestley-Taylor and Thornthwaite methods. For the
short term simulation (July 1983 to December 1990), a global net
radiation data set obtained from NASA facilitated making potential
evapotranspiration estimates using the Priestley-Taylor method.
For reasons discussed later in this paper, the Priestley-Taylor
method is considered superior to the Thornthwaite approach; however,
it is simpler to apply the Thornthwaite approach to long term
average conditions and to selected historical periods because
the global net radiation data used in this study are only available
from July 1983 to June 1991. It would be nice to have consistent
methods for estimating potential evapotranspiration over different
time periods so that fair comparisons can be made. Because the
Thornthwaite method is more easily applied over different historical
time periods, determining whether there are significant differences
between predicted runoff using the Priestley-Taylor and Thornthwaite
methods is an important question. The conclusion is that there
are significant differences and the Priestley-Taylor
approach is better. For this study, the average net radiation
over the eight year period when net radiation data were available was
taken to be the long term average net radiation. Both of the
Priestley-Taylor and Thornthwaite methods perform
poorly in arid regions and the significance of this is briefly
discussed.
Thornthwaite, 1948, first used the concept of potential
evapotranspiration as a meaningful measure of moisture demand
to replace two common surrogates for moisture demand temperature
and pan evaporation. Potential evapotranspiration refers to the
maximum rate of evapotranspiration from a large area completely
and uniformly covered with growing vegetation with an unlimited
moisture supply. There is a distinction between the term potential
evapotranspiration and potential evaporation from a free
water surface because factors such as stomatal impedence and plant
growth stage influence evapotranspiration but do not influence
potential evaporation from free water surfaces.
Brutsaert, 1982, notes on pp. 214 and 221 the remarkable similarity
in the literature among observations of water losses from short
vegetated surfaces and free water surfaces. He poses a possible
explanation that the stomatal impedance to water vapor diffusion
in plants may be counterbalanced by larger roughness values. Significant
differences have been observed between potential evapotranspiration
from tall vegetation and potential evaporation from free water
surfaces. The commonly used a value of 1.26 in the Priestley-Taylor
equation was derived using observations over both open water and
saturated land surfaces. For the most part, the term potential
evapotranspiration will be used predominantly in this paper and,
as used, includes water loss directly from the soil and/or through
plant transpiration.
An additional ambiguity in using the potential evapotranspiration
concept is that potential evapotranspiration is often computed
based on meteorological data obtained under non-potential conditions
(Brutsaert, p. 214). In this study, temperature and net radiation
measurements used for calculating potential evapotranspiration
in dry areas and for dry periods will be different than the values
that would have been observed under potential conditions. The
fact that the Thornthwaite and Priestley-Taylor methods have exhibited
weak performance at arid sites is related to this ambiguity because
the assumptions under which the expressions were derived break
down. Poor performance in arid regions is highly relevant to the
Niger Basin study because of large arid areas in the northern
part of the basin. This problem will be addressed a bit further
during the detailed discussions of each method.
Although not used directly in this study, a brief review of the
widely used Penman equation serves as a good starting point for
discussing the estimation of potential evapotranspiration.
Two requirements for evaporation to occur are an
energy input and a mechanism for the transport of water vapor
away from saturated surface. In light of this, two traditional
approaches to modeling evaporation are an energy budget approach
and an aerodynamic approach. With the energy budget approach,
the net radiation available at the surface (shortwave absorbed
plus longwave emitted) must be partitioned between latent heat
flux and sensible heat flux, assuming that ground heat flux is
negligible. This partitioning is typically achieved using the
Bowen ratio which is the ratio of sensible heat flux to latent
heat flux. Approximating the Bowen ratio typically requires measurements
of temperature and humidity at two heights. The aerodynamic approach
typically involves a vapor transport coefficient times the vapor
pressure gradient between the saturated surface and an arbitrary
measurement height. Determination of the vapor transport coefficient
typically requires measurements of wind speed, humidity, and temperature.
Brutsaert, Chow et al., and Dingman, present equations
for calculating the Bowen ratio and vapor transport coefficients.
Without simplifying assumptions, energy budget and the aerodynamic
methods require meteorological measurements at two levels.
In 1944, Penman combined the energy budget and aerodynamic approaches.
Penman's derivation eliminates the need for measuring water surface
temperature; only the air temperature is required. The resulting
equation is as follows:
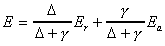
Er = 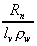
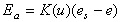
Rn is net radiation (typical units are W/m2),
lv is latent heat of vaporization (J/kg), row
is density of water (kg/m3), K(u) is a mass transfer coefficient,
es is saturated vapor pressure at air temperature,
and e is the actual vapor pressure.
The Penman equation is a weighted average of the rates of evaporation
due to net radiation (Er) and turbulent mass transfer
(Ea). Provided that model assumptions are met and adequate
input data are available, various forms of the Penman equation
yield the most accurate estimates of evaporation from saturated
surfaces. The "Evapotranspiration and Irrigation Water Requirements
Manual," ASCE, 1990, offers a performance comparison of twenty
popular methods for estimating potential evaporation. The top
six rated methods in ASCE, 1990, are forms of the Penman equation
(p.249).
Due to lack of data, it is not feasible to use the
complete Penman equation to make potential evaporation estimates
for the Niger Basin study. Because of their simplicity, the Thornthwaite
and Priestley-Taylor methods for estimating potential evaporation
are widely used in regional and global scale climatic water budget
studies. In the Niger Basin project, the only input data currently
available with adequate spatial coverage are temperature and net
radiation. While other simple temperature and/or radiation methods
are available and considered briefly later in this report, the
Thornthwaite and Priestley-Taylor methods are the focus of this
study.
A new global radiation data set makes using the Priestley-Taylor
method a feasible option for estimating potential evapotranspiration
at the scale of this study. Surface longwave and shortwave radiation
flux estimates are available for a 96 month period extending from
July 1983 to June 1991. The data are given on the ISSCP equal-area
grid which has a spatial resolution of 2.5 at the equator. Darnell
et al, 1992, assert that recent (last decade) advances
in input data and flux estimation algorithms have greatly improved
the ability to assess the radiation budget on a global scale.
Improvements in the input data come from the International Satellite
Cloud Climatology Project (ISCCP) and the Earth Radiation Budget
Experiment (ERBE). According to Darnell et al., 1995, longwave
flux estimates are accurate to within +/- 25 W/m2 and
Whitlock et al. estimate the accuracy of shortwave estimates
to be +/- 20 W/m2. The energy required to evaporate
1 mm/day of water is about 30 W/m2.
Global data sets of mean monthly temperature and
precipitation interpolated to a 0.5 by 0.5 grid were obtained
from Cort Willmott at the University of Delaware. These data are
from the "Global Air Temperature and Precipitation Data Archive"
compiled by D. Legates and C. Willmott. These monthly precipitation
estimates were previously corrected for gage bias. Data from 24,635
terrestrial stations and 2,223 oceanic grid points were used to
estimate the precipitation field. The climatology is largely representative
of the years 1920 to 1980 with more weight given to recent ("data-rich")
years (Legates and Willmott, 1990).
Daily precipitation and temperature estimates for stations
around the globe are available on a "Global Daily Summary"
CD-ROM produced by the National Climatic Data Center in Asheville,
NC. The period of record for these data is 1977-1991 although
not all stations have records for this entire period. The density
of climate stations is quite high in some parts of the Niger River
Basin but low in other areas. In addition, daily rainfall data for 191 stations in Niger and
41 stations in Mali were provided on floppy disk by FAO. The period
of record for these stations varies, but the most recent date
with available records from these stations is December 31, 1990.
A more detailed discussion of the data is provided in Part II
of this report.
A grid of water-holding capacity estimates was provided
by FAO for the Niger Basin project. Values in this grid were compiled
by an expert at FAO using information from the CD-ROM Digitized
Soil Map of the World (FAO, UNESCO, 1974-1981). There 6 unique
values of water-holding capacity (mm) in this grid: 0, 10, 30,
75, 125, and 200. The value zero is assigned to water bodies.
Monthly time series tables of precipitation and potential evaporation
for the period July 1983 to December 1990 were estimated at each
point on a regular mesh of 0.5 degree cells. This computational mesh
was selected because long term mean monthly estimates of rainfall
and temperature at these points were obtained from C.J. Willmott at the University
of Delaware. The mean monthly values from Willmott were used in
conjunction with thiessen polygons to create 0.5 surfaces of precipitation
and potential evaporation for each month in the short-term study
period. The basic methodology is described here and more details
are provided in Part II of this report.
The initial approach for creating monthly precipitation surfaces
was as follows: (1) Created thiessen polygons based on selected
precipitation stations and used these polygons to associate each
0.5 computational cell with a given station. (2) Calculate the
monthly value in cell i and historical month m with the following
equation:
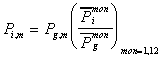
The subscript i indicates cell index where precipitation is being
estimated and g indicates value at the gage. The superscript "mon"
indicates a monthly average value obtained from the Legates and
Willmott climatology. If the mean value at the gage is zero, then
the ratio 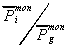
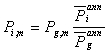
An attempt to distribute daily rainfall values in a similar manner
to the monthly values was made, but in locations where our precipitation
gage network is sparse, this involves the poor assumption that
individual rainfall events occur over very large areas. Thus,
daily calculations made using this approach were not put to use
as input to the flow simulation model. One approach to dealing
with this problem would be to use a library of dimensionless daily
time series distributions to distribute monthly rainfall totals
for each cell throughout a month; however, because the merits
of adopting this approach are unclear and because it involves
a large degree of complication, it was not pursued.
In 1972, C.B. Priestley and R.J. Taylor showed that,
under certain conditions, knowledge of net radiation and ground
dryness may be sufficient to determine vapor and sensible heat
fluxes at the Earth's surface. When large land areas (on the order
of hundreds of kilometers) become saturated, Priestley and Taylor
reasoned that net radiation is the dominant constraint on evaporation
and analyzed numerous data sets to show that the advection or
mass-transfer term in the Penman combination equation tends toward
a constant fraction of the radiation term under "equilibrium"
conditions. According to Brutsaert, 1982, Slatyer and McIlroy,
1961, first defined the concept of equilibrium evaporation as
a state that is reached when a moving air mass has been in contact
with a saturated surface over a long fetch and approaches vapor
saturation -- thus causing the advection term in the Penman equation
to go to zero. Both Slatyer-McIlroy and Priestley-Taylor considered
the radiation term in the Penman equation to be a lower limit
for the evaporation from a moist surface. The form of the evaporation
equation developed by Priestley and Taylor is as follows, a constant
(alpha) times
Penman's radiation term.
Priestley-Taylor estimates have shown good agreement with lysimeter
measurements for both peak and seasonal evapotranspiration in
humid climates; however, the Priestley-Taylor equation substantially
underestimates both peak and seasonal evapotranspiration in arid
climates. The advection of dry air to irrigated crops is likely
to be greater in arid climates because large saturated areas are
rare, resulting in a more dominant role of the advection term.
A higher alpha
coefficient may be required in arid climates (ASCE, 1990). Based
on arid sites studied in ASCE, 1990, a value of alpha=1.7-1.75
seems more appropriate for arid regions. Shuttleworth, 1993, states
that the Priestley-Taylor method is the "preferred radiation-based
method for estimating reference crop evapotranspiration."
Shuttleworth, 1993, notes that errors using the Priestley-Taylor
method are on the order of 15% or 0.75 mm/day, whichever is greater,
and that estimates should only be made for periods of ten days
or longer.
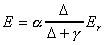
Equating this expression to the combination equation reveals that
the advection term must be a constant fraction of the radiation
term if alpha
is a constant.
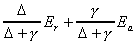
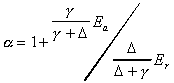
Using micro-meteorological observations over ocean surfaces and
over saturated land-surfaces following rainfall, Priestley and
Taylor came up with a best-estimate of 1.26 for the parameter
alpha. The fact that alpha
is greater than one indicates that true advection-free conditions
do not exist. Since 1972, several other researchers have confirmed
that alpha values
in the range 1.26-1.28 are consistent with observations under
similar conditions. Some researchers have found significantly
lower values for the alpha
coefficient, but these coefficients were found for different types
of surfaces (i.e. tall vegetation or bare soil as opposed to grass
and open water). There have also been indications that the alpha
coefficient may exhibit significant seasonal
variation (Brutsaert, p. 221).
The Jensen-Haise, FAO-24 Radiation, and the Turc
method are all classified as radiation-based methods in ASCE,
1990, but the FAO-24 Radiation Method and the Turc method require
basic information beyond temperature and net radiation mean humidity
and mean wind speed for FAO-24 and mean humidity for the Turc
method. The Jensen-Haise method does receive an overall ranking
higher than the Priestley-Taylor method in ASCE 1990, Table 7.20;
however, the Priestley-Taylor equation outranks the Jensen-Haise
equation for humid climates. Predicted surplus volumes are much
more sensitive to the accuracy of the potential evaporation estimate
in humid climates than arid climates; therefore, the Priestley-Taylor
approach is considered a better choice than Jensen-Haise for our application. It is
also noteworthy that the Jensen-Haise, FAO-24 Radiation, and the
Turc method all use the incoming shortwave radiation rather than
net radiation as an input. In theory, net radiation is a better
indicator of potential evaporation than shortwave radiation because
variations in albedo and cloudiness have already been taken into
consideration.
Thornthwaite (1948, Wilm et al., 1944) developed
an empirical equation for estimating potential evapotranspiraion
from a reference grass surface that requires only mean monthly
temperature and day length estimates as input. The regression
equation was developed using data from lysimeter and small watershed
water balance experiments at several sites scattered throughout
the United States. Thornthwaite recognized that there is a more
direct physical relationship between potential evaporation and
net radiation than between potential evaporation and temperature,
but foresaw correctly that sufficient radiation measurements or
accurate calculations to reliably estimate potential evaporation
would be difficult to come by for many years to come. Using temperature
as a surrogate for net radiation involves the implicit assumptions
that albedo is constant, the rate of evapotranspiration is not
influenced by advection of moist or dry air, and that the Bowen
ratio is constant. These conditions do not exist in arid and semi-arid
regions except during short periods after regional rain storms
(ASCE, 1990). The comparison and ranking of potential evaporation
estimating methods in the ASCE Manual (Table 7.18) clearly
shows the poor performance of the Thornthwaite methodology in
arid climates.
Mintz and Walker discuss the fact that the Thornthwaite equation
was developed for temperatures measured under potential conditions
and only represents "true" potential evaporation when
there is no soil moisture stress. Application in locations with
soil moisture stress results in an "apparent" potential
evaporation. The energy balance at the land surface and thus the
surface temperature are altered under non-potential conditions.
Mintz and Walker observe that dry areas have higher temperatures
than wet areas at the same latitude and season and develop an
empirical equation that relates the potential air temperature
to the measured air temperature. Based upon measured air surface
temperatures, the Thornthwaite method will overestimate the "true"
potential evaporation in arid regions. Mintz and Walker assert that the largest difference between calculated
"true" and "apparent" potential evaporation
occurs in the central Sahara where "apparent" is 6.2
mm/day in July and the "true" is 5.5 mm/day.
Willmott et al., 1985 summarize the Thornthwaite evaporation
equations as follows.
During the course of this investigation, a FORTRAN code for computing
water budgets called "WATBUG" obtained from Cort J.
Willmott at the Universtiy of Delaware (Willmott, 1977) has been
very helpful. The WATBUG code allows for daily or monthly budgeting
and includes subroutines for balancing, computing day length given
latitude, and calculating potential evaporation with the Thornthwaite
equation. All or parts of the WATBUG routine have been used in
this investigation, either in their original or modified form.
An Avenue script for use with monthly data that uses the budgeting
scheme of Equation 3 has also been written.
Potential evapotranspiration (PE) in (mm/month) without adjustment
for day length is computed with:
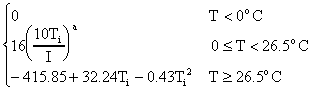
where T is mean surface air temperuture in month i (°C) and
I is the heat index defined in Equation 13 below. The exponent
a in Equation 12 is a function of the heat index (I).
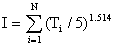
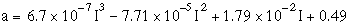
Monthly estimates of potential evapotranspiration calculated with
Equation 12 need to be adjusted for day length because 30 day
months and 12 hour days were assumed when this relationship was
developed.
The adjusted potential evaporation accounting for month length
and daylight duration is given by
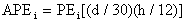
where APE is in (mm/month), d is length of the month in days,
and h is the duration of daylight in hours on the fifteenth day
of the month.
This empirical temperature-based method requires
only mean monthly temperatures and an estimate of the monthly
percentage of annual daytime hours. Based upon the results in
ASCE, 1990, Tables 7.18 and 7.19, this method outperforms the
Priestley-Taylor method in all months and in the peak month for
arid regions but exhibits poor performance in humid regions.
Figure 1 shows the spatial distribution of monthly average (90
months) potential evapotranspiration (PE) predicted using the
two methods. ( Click here to view
all of Figure 1.; Zoom in on top map , and
bottom map in Figure 1.) There are clear differences in the PE spatial variations.
The Priestley-Taylor PE estimates show decreasing trend from high
values in the humid south portions to lower values in the arid
north. The Thornthwaite estimates exhibit no consistent trend.
On a basin average, the Thornthwaite PE (136.8 mm/month) is higher
than the Priestley-Taylor PE (114.1 mm/month). Figure 2 shows
the variation in monthly PE throughout the year (7 year average)
for the cells identified in Figure 2. ( Click here to view
all of Figure 2.; View top , middle ,
and bottom charts in Figure 2 respectively.)
Moving south to north, seasonal
trends of higher PE in the summer show up. This is related to
the fact that most of the rainfall occurs in the summer and relatively
less rainfall occurs during other parts of the year as you move
north. Net radiation is higher in wet months because more solar
radiation is absorbed. Moving south to north, Thornthwaite PE
becomes larger relative to Priestley-Taylor PE. This is the reason
that the Thornthwaite method actually yields higher average surplus
despite having a higher basin-average PE (Figure 3). Figure 3
shows a comparison of mean annual surplus values computed from
the soil-water budget using the two different estimates for PE.
( Click here to view
all of Figure 3.; Zoom in on top , middle ,
and bottom maps in Figure 3 respectively.)
Because the Priestley-Taylor PE is higher in the south where all
the rainfall occurs, the actually evaporation estimated using
this method is greater and the average surplus generated is smaller.
It is clear from the discussion of errors above that potential
evaporation estimation errors can easily be on the order of 1
mm/day. This seemingly small error can yield significant differences
in surplus volumes, and surplus calculations are especially sensitive
to the spatial pattern of potential evapotranspiration estimates.
The seasonal pattern of PE may also play a significant role in
surplus generation, but no definite conclusions have been made
from this brief study.
Three reasons for favoring the Priestley-Taylor method over the
Thornthwaite method are (1) net radiation has a more direct physical
relationship to evaporation, (2) the Priestley-Taylor method receives
a higher ranking than the Thornthwaite method in comparison to
lysimeter estimates (ASCE, 1990), and (3) the spatial pattern
of Priestley-Taylor PE estimates in the Niger basin are more sensible.
The range of errors in net radiation estimates (in units of mm/day)
are of similar magnitude to the differences in Priestley-Taylor
and Thornthwaite PE.
Estimated basin mean surplus volume is very sensitive to method
of calculating PE. The ratio of Thornthwaite basin mean surplus
to Priestley-Taylor basin mean surplus is 1.7. The formulation
of Equation 3 should be less sensitive to PE than the formulation
of Equations 16 and 17.
The surplus results presented in Figure 3 were computed using
a slightly different methodology than that described in Equation
3. This earlier analysis used the methodology of C.J. Willmott
written in the WATBUG FORTRAN code. The methodology can be summarized
as follows:
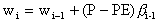
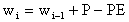
If wi > w*, then surplus for that day is wi-w*
and wi is set equal to w*. In addition to the fact
that it does not inclued the rainfall extraction term, Equation
16 differs from Equation 3 because it involves the assumption
that if precipitation is less than potential evaporation then
all precipitation used to satisfy the potential demand is consumed
immediately, before having a chance to enter the soil. This generates
less surplus than the approach described in Equation 18 which
is the same as Equation 3 without the rainfall extraction term.
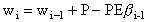
Variables in Equation 18 are subject to the same constraints as
in Equation 3.
As of 1992-93, Mintz and Walker used the Thornthwaite approach for
PE calculations because they were skeptical about our knowledge
of global net radiation, either from direct measurements or calculations,
and thus didn't envision the application of the Penman, Budyko,
or Priestley-Taylor approaches directly on a global basis. Mintz
and Walker indicate that the Thornthwaite and Priestley-Taylor
methods are consistent to within +/- 0.5 mm/day or 15 mm/month
in any given month. However, Figure 2 indicates differences of
up to 50 mm/month or more in Cell 3. Recall that the accuracy
of the of the radiation fluxes are about +/-20-25 W/m2 which corresponds
to about 0.7 mm/day or 21 mm/month. Shuttleworth puts the accuracy
of the Priestley-Taylor method at about 0.75 mm/day.
Several figures are included here to try to illustrate
some of the results. Figure 4 illustrates the mean annual surplus
for the long term and short term cases.( Click here to view
all of Figure 4.; Zoom in on top map , and
bottom map in Figure 1.) Figure 5 shows the conversion
of cell surplus values to watershed average values. Figure 6 illustrates
the computed time series of surplus for several cells, and Figure
7 illustrates all components of the soil-water balance at a cell. ( Click here to view
all of Figure 7.; Zoom in on precipitation , potential evaporation ,
evaporation , soil moisture , and surplus .)
The names of the coverages and data files containing surplus results
are provided in Part II, Section II of this report.
Alley, W.M., "On The Treatment Of Evapotranspiration,
Soil Moisture Accounting, And Aquifer Recharge In Monthly Water
Balance Models," Water Resources Research, 20,1137-1149,1984
ASCE, Evapotranspiration and Irrigation Water
Requirements, Jensen, M.E., R.D. Burman, and R.G. Allen (editors),
ASCE Manuals and Reports on Engineering Practice No. 70, 1990.
Brutsaert, W., Evaporation into the Atmosphere:
Theory, History, and Applications, D. Reidel Publishing Company,
Dordrecht, Holland, 1982.
Chow, V.T., D.R. Maidment, and L.W. Mays, Applied
Hydrology, McGraw-Hill, Inc., New York, NY, 1988.
Darnell, W.L., W.F. Staylor, S.K. Gupta, N.A. Ritchey,
and A.C. Wilber, "Seasonal Variation of Surface Radiation
Budget Derived from ISCCP-C1 Data," J. Geophysical. Res.,
97, 15741-15760, 1992.
Darnell, W.L., W.F. Staylor, S.K. Gupta, N.A. Ritchey,
and A.C. Wilber, "A Global Long-term Data Set of Shortwave
and Longwave Surface Radiation Budget," GEWEX News, 5,
No.3, August 1995.
Dingman, S.L., Physical Hydrology, Prentice Hall, Inc., Englewood Cliffs, NJ, 1994.
Dyck, S., "Overview on the Present Status of
the Concepts of Water Balance Models," IAHS Publ. 148,
Wallingford, 3-19, 1983.
Gutman, G., and L. Rukhovetz, "Towards Satellite-Derived
Global Estimation of Monthly Evapotranspiration Over Land Surfaces,"
Adv. Space Res., 18, No. 7, 67-71, 1996.
Legates, D.R., and Willmott, C.J., "Mean Seasonal
and Spatial Variability in Gauge-Corrected, Global Precipitation,"
International Journal of Climatology, 10, 111-127,
1990.
Maidment, D.R., McKinney, D., Lindner, R., Olivera,
F., Reed, S., Zichuan, Y., "Water Balance of the Niger Basin
: Interim Report," Prepared for the United Nations Food and
Agricultural Organization and UNESCO by the Center for Research
in Water Resources University of Texas at Austin, July 1995.
Manabe, Syukuro, "Climate and the Ocean Circulation:
I. The Atmospheric Circulation and the Hydlrology of the Earth's
Surface," Monthly Weather Review, 97, No. 11,
Nov. 1969.
Mather, J.R., The Climatic Water Budget, Lexington
Books, 1972.
Mintz, Y., and Serafini, Y.V., "A Global Monthly
Climatology of Soil Moisture and Water Balance," Climate
Dynamics, 8, 13-27, 1992.
Mintz, Y., and G.K. Walker, "Global Fields of
Soil Moisture and Land Surface Evapotranspiration Derived from
Observed Precipitation and Surface Air Temperature," J.
Applied. Meteor., 32, 1305-1334, 1993.
NCDC, "Global Daily Summary," 1977-1991,
CD-ROM, Asheville, NC.
Penman, H.L., "Natural Evaporation from Open
Water, Bare Soil and Grass," Proc. R. Soc. London, Ser.
A, 193, 120-145, 1948.
Priestley, C.H.B., and R.J. Taylor, "On the
Assessment of Surface Heat Flux and Evaporation Using Large-Scale
Parameters," Monthly Weather Review, 100, No.
2, 81-92, February 1972.
Shuttleworth, J.W., "Evaporation," Handbook
of Hydrology, D.R. Maimdent Editor, McGraw-Hill, Inc., 1993.
Thornthwaite, C.W., "An Approach Toward a Rational
Classification of Climate," Geographical Review, 38,
55-94, 1948.
Whitlock et al., "First Global WCRP Shortwave
Surface Radiation Budget Data Set," Bull. Amer. Meteor.
Soc., 76, 6, 905-922, 1995.
Wilm, H.G., C.W. Thornthwaite, E.A. Colman, N.W.
Cummings, A.R. Croft, H.T. Gisborne, S.T. Harding, A.H. Hendrickson,
M.D. Hoover, I.E. Houk, J. Kittredge, C.H. Lee, C.G. Rossby, T.
Saville, and C.A. Taylor, "Report of the Committee on Transpiration
and Evaporation, 1943-44," Transactions, American
Geophysical Union, 25, 683, 1944.
Willmott, C.J., C.M. Rowe, and Y. Mintz, "Climatology
of the Terrestrial Seasonal Water Cycle," Journal of Climatology,
5, 589-606, 1985.
Willmott, C.J., "WATBUG: A FORTRAN IV Algorithm for Calculating the Climatic Water Budget," Publications in Climatology, 30, 2, 1977.