Internet students can download the necessary files.
(2) Answer other questions about the analysis that you perform as noted on the instructions in the following pages.
To begin this exercise, you need to be working at a machine with Arcview 2.0 or 2.1 operating and have access to the sample data files which are stored in \gisfiles\ex2af . These files include the themes:Afrbord, Cities, Deg30, Latlong, World94.

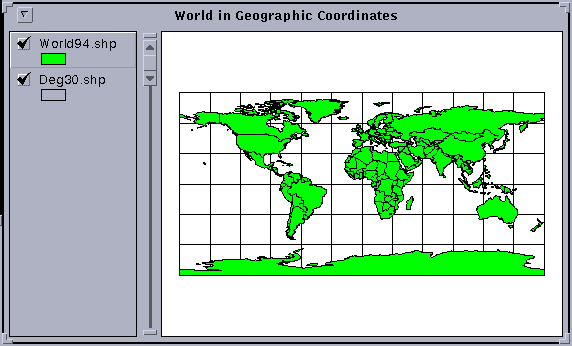
Move the cursor around on the view and you will see a pair of numbers above the view on the toolbar to the right of "scale" that alter as you move the cursor. These give the location of the cursor and from the values displayed you can see that these coordinates are given in decimal degrees of latitude and longitude.
Questions: what is the spatial extent of the view shown in terms of degrees of latitude and longitude? Where is the point (0,0) latitude and longitude located on the earth's surface? What does this location represent?
Click on View/Properties and you will see a window open with options for Projection. Click on the Projection button. Under Projections of the World you'll see a projection Type labeled Robinson. Click OK in the two open windows and you'll see the View transformed to appear in a Robinson projection, which is a relatively new style of map projection for the earth designed to present the whole earth with a minimum of distortion at any location. If you move the cursor over this space, you'll see that the coordinates are now in a very different set of units, meters in the projected coordinate system.
Go back to View/Properties and under Projection Type, click on the arrow to the right of Robinson, which opens a display window, from which you can select Geographic. Click, OK, OK, and the View will be transformed back to the appearance that it had originally.
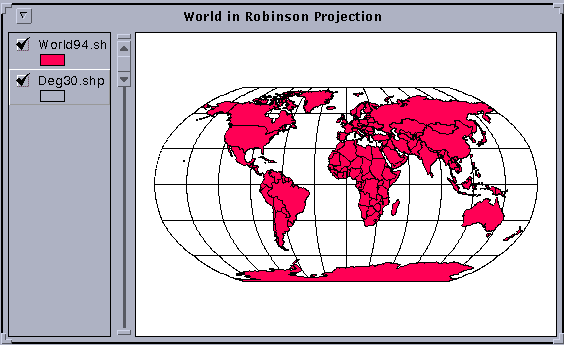
Go back to View/Properties and reproject the View into the Robinson projection. Here is an image of the world in the Robinson Projection. To label your view World in Robinson Projection like that shown in the picture, use View/Properties to change the Name field, as before.
Go to the View/Properties sequence and this time under projection Type, select View from Space (the last option in the list of Projections of the World). You'll see a nice 3-D view of the globe as seen from a viewpoint above Massachusetts, USA. If you want to see how the world looks when viewed from above Rabat, Morocco, go back to the projection selection window, click on Custom and then type -7 for the Central Meridian and 32 for the reference latitude (the projection name changes to "Orthographic" when you do this). And there is the world centered on Rabat, Morocco! Change the view name to World from Above Rabat, Morocco using the same procedure as before.
Add the Cities.shp theme to the view, and select You may wish to try looking at the world from a few other places. You can get the coordinates of locations on the earth by viewing earth in the geographic projection. Play around a bit and have some fun!
Here is what a view of the World from Space above Rabat, Morocco would
look like. 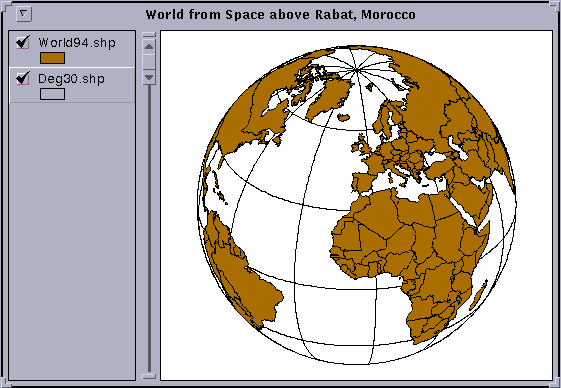
Label the Views of the World with the Text Tool ![]() in the lower tool bar. If your labeling is too small (the default is 14
point), use Window/Show Symbol Palette to bring up the Palette,
click on the button labeled ABC to get the Font Palette and then resize
the lettering to perhaps 24 or 36 point. If you want to color the lettering,
choose the Paintbrush icon in the Tool Palette, and in the Color Palette,
scroll forward from Foreground to Text, then choose the color for the text.
Label some of the main meridians and parallels in the geographic coordinate
view.
in the lower tool bar. If your labeling is too small (the default is 14
point), use Window/Show Symbol Palette to bring up the Palette,
click on the button labeled ABC to get the Font Palette and then resize
the lettering to perhaps 24 or 36 point. If you want to color the lettering,
choose the Paintbrush icon in the Tool Palette, and in the Color Palette,
scroll forward from Foreground to Text, then choose the color for the text.
Label some of the main meridians and parallels in the geographic coordinate
view.
If possible, make a printout of the Layout. Save the Project (File/Save Project As) so that you don't have to recreate it again later if you need it again.
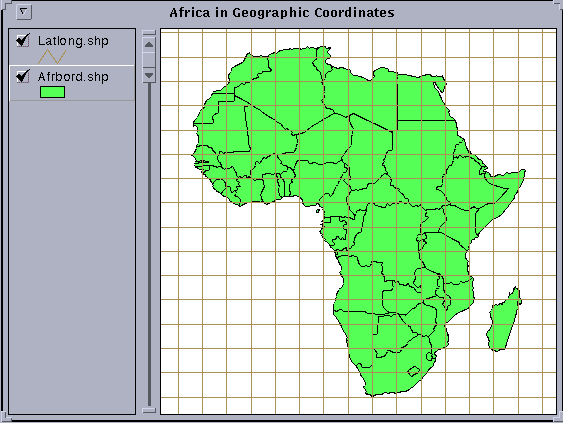
Question: What is the geographic extent of Africa? Give the East
and West limits of longitude for Africa and those for the Northern and
Southern extent of the continent to the nearest degree. Identify the Equator
and use the ![]() tool (make afrbord.shp
the active theme and double-click on a map polygon with this tool selected)
to determine the names of the countries that the Equator passes through
in Africa. If we removed a vertical slice out of the world cut along the
meridians defining the most Eastern and Western points in Africa, how much
of the globe would we have cut out?
tool (make afrbord.shp
the active theme and double-click on a map polygon with this tool selected)
to determine the names of the countries that the Equator passes through
in Africa. If we removed a vertical slice out of the world cut along the
meridians defining the most Eastern and Western points in Africa, how much
of the globe would we have cut out?
Create a new View, View2, and add Afrbord.shp and Latlong.shp to the View as you did previously. Go to View/Properties and ensure that Map Units are labeled decimal degrees since the View that you are looking at is in Geographic Coordinates. Hit Projection, select Custom, and among the projection choices offered, select the Transverse Mercator projection. Choose 20 as the central meridian, click OK, and OK. You can zoom in on Africa to produce an image like the one shown below. Note that the meridian at 20 E is the only straight meridian, all other meridians are curved lines.
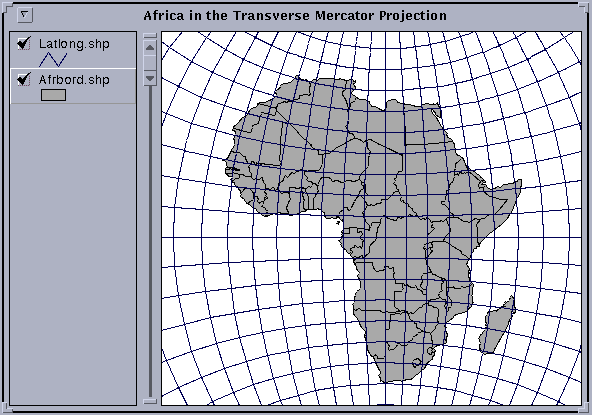
Label the Views of Africa with the Character Tool (Labeled T in the lower tool bar). If your labeling is too small (the default is 14 point), use Window / Show Symbol Palette to bring up the Palette, click on the button labeled ABC to get the Font Palette and then resize the lettering to perhaps 24 or 36 point. Label some of the main meridians and parallels in the geographic coordinate view.
If possible, make a printout of the Layout. Save the Project (File/Save Project As) so that you don't have to recreate it again later if you need it again.
To select only Morocco, a special display of the Africa theme can be set up as follows:
([Name] = "Morocco")
If you don't have all the components of the query built correctly, hit Cancel in the Query Builder window and start again to build the query.
Here is an image of Morocco in geographic coordinates.
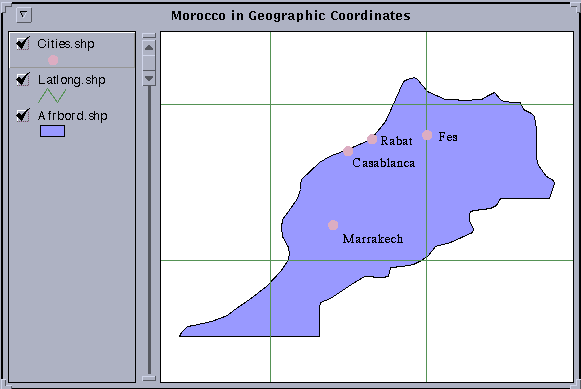
The latitude/longitude grid displayed is at 5 degree intervals of latitude
and longitude. To determine what latitude or longitude a particular line
represents, highlight the theme latlong.shp in the Legend bar and use the
Information tool ![]() in the tool
bar. As you click on each line a small display window will give you the
record of information about that line. You can use the same tool to determine
the names of the cities in cities.shp (remember to make cities.shp the
active Theme to make this work).
in the tool
bar. As you click on each line a small display window will give you the
record of information about that line. You can use the same tool to determine
the names of the cities in cities.shp (remember to make cities.shp the
active Theme to make this work).
Create a new View (View2), add afrbord.shp and latlong.shp to it, and select only Morocco for display as before.
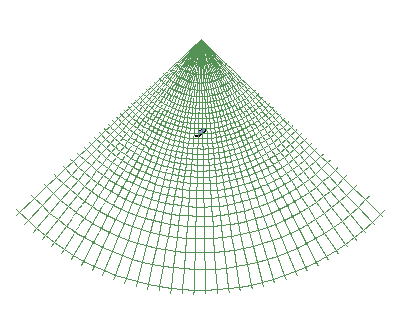
To view Morocco in the Lambert Conformal Conic projection, highlight the afrbord.shp theme, go to View/Properties, set the map units to Decimal Degrees, and click on the Projection bar, click on Custom and in the Projection Properties window displayed, select Projection: Lambert Conformal Conic. Set the Central Meridian to -7, set Standard Parallel 1 to 29, Standard Parallel 2 to 34.5, and the reference latitude to 25. Click OK at the two display windows to transform the view to the projected domain. Notice how the meridians now fan out from an origin at the center of rotation of the earth (a consequence of using a conic projection centered on the axis of rotation of the earth). The display shown is that which would be produced by cutting the cone up the back side and unfolding the cone so that it lays flat on the table.
Here is an example of the Lambert Conformal Conic Meridians and Parallels
Morocco is a dark dot in the center of the meridians. Use the Zoom tool to highlight Morocco. The Central Meridian used for this projection was 7 W, which would appear as a vertical line, if present, on the display. A closer view of Morocco is shown below.
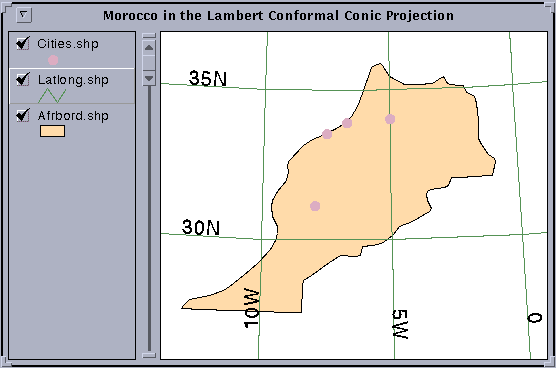
Create a new View (View3), add afrbord.shp and latlong.shp to it, and select Morocco as before.
To view Morocco in the Albers Equal-Area projection, highlight the afrbord.shp theme, go to View/Properties, set the map units to Decimal Degrees, click on the Projection bar, click on Custom and in the Projection Properties window displayed, select Projection: Albers Equal-Area Conic. Set the Central Meridian to -7, set Standard Parallel 1 to 29, Standard Parallel 2 to 34.5, and the reference latitude to 25. Click OK at the two display windows to transform the view to the projected domain. The image that you see looks very similar to that produced by the Lambert projection.
If you take a 5 degree box of latitude and longitude, such as one of those shown in the views, the ratio of the East-West distance between meridians to the North-South distance between parallels is Cos (latitude) : 1. For example, at 30 degrees N, Cos(30) = 0.866, so the ratio is 0.866 : 1, at 45 degrees N, Cos(45) = 0.707, so the ratio is 0.707 : 1. In the projected Albers view (View3), the result is that square boxes of latitude - longitude appear as elongated quadrilaterals with a longer base than their top edge. This elongation becomes more evident as you move closer to the poles. You can see this if you zoom out from Morocco. In geographic coordinates, the effect of the real convergence of the meridians is lost because the latitude and longitude grid form a set of perpendicular lines.
Label the Views of Morocco with the Text Tool (Labeled T in the lower tool bar). If your labeling is too small (the default is 14 point), use Window/Show Symbol Palette to bring up the Palette, click on the button labeled ABC to get the Font Palette and then resize the lettering to perhaps 24 or 36 point. Label some of the main meridians and parallels in the geographic coordinate view.
Make a printout of the Layout. Save the Project (File/Save Project As) so that you don't have to recreate it again later if you need it again.
Another one done!!
These materials may be used for study, research, and education, but please credit the authors and the Center for Research in Water Resources, The University of Texas at Austin. All commercial rights reserved. Copyright 1997 Center for Research in Water Resources.