Floodplain Modeling in the Waller Creek Watershed: Austin, Texas
Rebecca C. Smyth, Bureau of Economic Geology, University of Texas at Austin
CE394K.2 Term Paper (Revised)
May 8, 2001
INTRODUCTION
The Hydrologic Engineering Center-River Analysis System (HEC-RAS) model is a surface water flow model developed by the Army Corp of Engineers for the Hydrologic Engineering Center. In this program one-dimensional steady flow hydraulics (one-dimensional water surface profile calculations) are used to generate flood hazard maps. In simple terms, the model uses surface water flow data to predict water-surface elevations. These elevations are then posted on a terrain model to see where flooding will most likely occur.
HEC-RAS requires a terrain model with three-dimensional attributes (x, y, and z) for the area of interest. The terrain model commonly used in hydrologic modeling is a Triangulated Irregular Network (TIN). HEC-GeoRAS is a pre- and post-processing program developed cooperatively by the Hydrologic Engineering Center (HEC) and the Environmental Systems Research Institute Inc. (ESRI) to (1) extract geometric data from a TIN for input into HEC-RAS and (2) take output from the model and generate a water surface elevation TIN that can be superimposed on the terrain TIN to identify flood-prone areas. I have used the HEC-GeoRAS extension to ArcView and HEC-RAS 2.2 to complete a modeling exercise developed by (Snead and Maidment (2000).
Geometric data required for input into the model include elevation cross sections extracted from the TIN and located at specific places along the reach or reaches being modeled. In addition to presenting the results of the HEC-RAS modeling exercise, I also show a comparison of cross sections derived from the Campus-Area Waller Creek Watershed TIN terrain model and from LIDAR digital elevation data generated at the University of Texas at Austin, Bureau of Economic Geology (UTBEG).
LIDAR is an acronym for Light Detection and Ranging; it is a method for very accurately mapping surface elevations. The UTBEG recently purchased an All-Terrain Laser Mapper (ALTM), a LIDAR-based instrument that when mounted on a small aircraft can collect x, y, and z data used to generate digital elevation models (DEM) with grid nodes spaced as closely as one meter. Before spatial data collected using LIDAR can be used in a hydrologic model, we must complete multiple stages of data processing. These include: (1) compute a differentially corrected aircraft trajectory using Global Positioning System (GPS) software, (2) combine several synchronized data streams collected by the ALTM with the GPS trajectory to generate the raw x, y, and z data, (3) grid the data to generate an "all-points DEM", (4) filter the raw data and re-grid to generate a "vegetation-removed DEM", and (5) adjust the grids to compensate for the differences between ellipsoidal and orthometric heights.
HEC-RAS MODEL EXERCISE
The two categories of input required for the HEC-RAS model are Geometric Data and Flow Data.
The steps required to complete the hydrologic modeling exercise are:
Terrain Model Processing
The TIN terrain model used in the hydrologic modeling exercise was generated by Esteban Azagra-Camino during graduate studies in the Civil Engineering Department at the University of Texas at Austin (http://www.ce.utexas.edu/prof/maidment/grd/azagra/home.htm). Information about this TIN are outlined below.
Information about the "walterrain" TIN
Area covered: 36,000,000 ft2 or 1.29 mi2
Number of triangles: 332,120
Average area covered by a triangle: 108 ft2
Elevation range: 481.23 to 902.9 ft
HEC-Geo-RAS Preprocessor
Geometric data include a river system schematic and cross section data. These data are extracted from the TIN using the HEC-GeoRAS preprocessor. The geometric data to be defined in order to complete the preprocessing for HEC-RAS include:
You start by defining polylines (lines drawn in plan view on the TIN image)then use these to extract the 3D attributes (elevation values) from the TIN model. Details of the modeled reaches and one example cross section are given below.
Stream center line Attributes (Streamcl3d.shp)
Number of routing reaches: 3
River stations on each reach: WallerUS (upstream tributary of Waller Creek)- from 3331.235 to 7768.374ft; WallerDS (downstream tributary of Waller Creek) - from 0.0 to 4437.139ft; Trib (Waller Creek tributary)- from 0.0 to 4437.139ft.
Total river length: 11,327.522ft
Information about cross section 44 (attributes of Xcutlines.shp)
Location: second cross section from top of page on east side of TIN (left fork)
Reach ID: Trib
Station: 3219.9059
Left bank is 52.7% of the way across the cross section
Right bank is 59.7% of way across the cross section
Distance to next downstream cross section: 313ft (difference between station numbers of two adjacent cross sections.
The last step of HEC-GeoRAS pre-processing is to prepare the HEC-RAS Import File.
HEC-RAS Steady State Simulation
The necessary input for a HEC-RAS steady state simulation is two sources of data (1) geometric data derived from TIN using GeoRAS and (2) flow data which in this case are derived from HEC-HMS and provided for the exercise. Shown below is an example cross section and a list of the pertinent associated data.
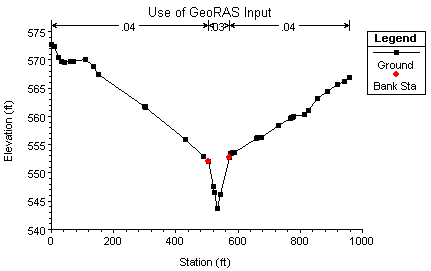
Information obtained from Station 3219.9059 cross section in HEC-RAS (figure 1)
Width: 900ft
Mannings h values: 0.03 in channel; 0.04 on banks.
Distance from left end of cross section to: left bank = 504.82ft, right bank = 569ft.

Figure 1. Cross section number 44 on the Waller Creek Tributary
Steady Flow Data from a 100-yr Storm are provided as the flow data input for the modeling exercise. Development of Steady Flow data requires input of the following parameters:
Running HEC-RAS Steady Flow Simulation
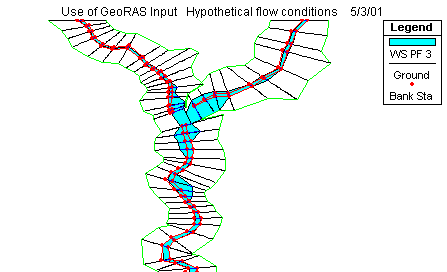
Figure 2. Extent of flooding using profile 3 water level elevations.
HEC-GeoRAS Post Processing
This incorporates the water surface profile data into a water surface TIN, which is superimposed onto the terrain elevation TIN for 2D or 3D visualization of the flooded areas.
Complete the following steps:
Information on water surface elevations
Range: 553ft at northern (upstream) end; 498ft at southern (downstream) end.
Information on flood plain delineation
Deepest floodwater: 14.64 to 16.47ft
Location: southern edge of TINs (downstream end)
The exercise includes deletion of 5 low elevation polygons, but does not include extending lengths of limiting cross sections on the tributary (figure 3).
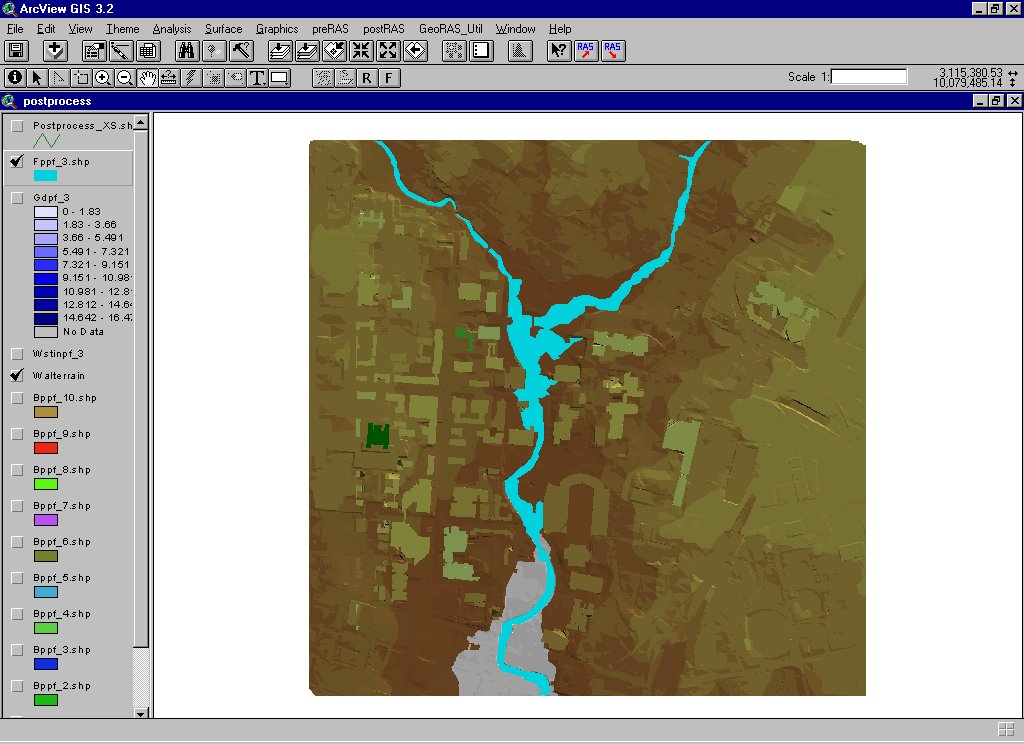
Figure 3. Completed Floodplain Map Featuring Shape Theme as opposed to Grid Theme.
3-D Floodplain Development
The objective is to utilize the ArcView 3D Analyst extension to view the results in three dimensions (figure 4).
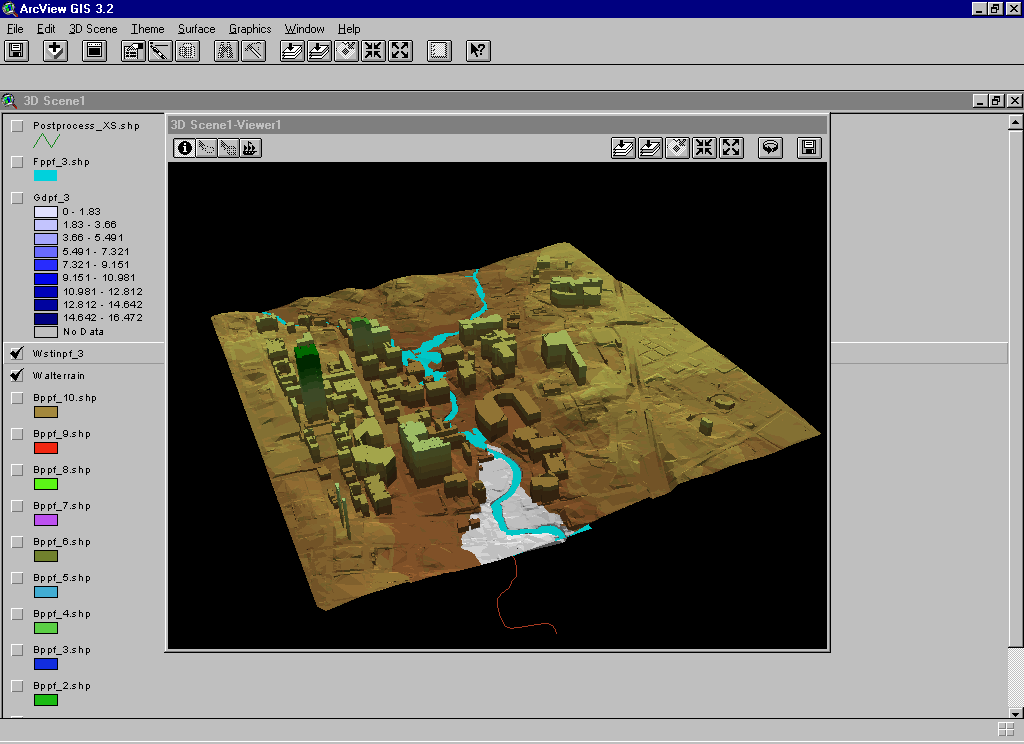
Figure 4. Three dimensional view of Waller Creek in the Campus Area
COMPARISON OF CROSS SECTIONS GENERATED FROM TIN VERSUS LIDAR
General Discussion of LIDAR and Vegetation Removal
The steps required to process LIDAR data so that it can be used in a hydrologic model include, but are not limited to:
The three dimensional attributes of LIDAR data are displayed using images created from DEMs. A DEM is a regular grid of elevation data. It is the simplest way to represent topography in a digital format (http://www.geog.ubc.ca/courses/klink/gis.notes/). I generated DEMs and shaded relief maps for this term project using the commercial software, Surfer. Kriging, Natural Neighbor, and Minimum Curvature are among the many different methods for gridding; here I used Minimum Curvature with a 1m data spacing. For the hillshaded images I used 135 and 45 degrees for horizontal and vertical light position angles, respectively.
One of the ALTM data streams consists of range measurements. The time difference between when the wave, travelling at the speed of light (~3 x 108 m/sec), is emitted and returned gives the range to a target. Targets can be particles in clouds immediately underneath the aircraft, tops of buildings or vegetation, intermediate levels in a layered forest, or the ground surface. The laser pulse emitted from the ALTM has a distinct signature. Because the laser pulse diameter (spot size) can be as large as 25cm when it hits a target, different portions of the signal may reflect off of objects at different ranges from the aircraft. The result is a returned signal that is diffuse or spread out in time. Very precise time interval meters in the ALTM record the first and last portions of each returned laser pulse. The name for these two portions of the returned signal, first pulse and last pulse, is misleading because they are both part of a single laser pulse. If a single laser pulse hits partially on the edge of a building and partially on the ground, the first pulse will represent the range to the top of the building and the last pulse will represent the ground elevation.
Filtering of raw LIDAR data to remove vegetation is a complicated process for which there are several different approaches. The approach that would give the best results should utilize the time differences between first and last pulse returns. One of the difficulties BEG has encountered with LIDAR data filtering is the inability to remove vegetation without decimating buildings. Figure 5 shows shaded relief images generated from a 1-m DEM of a portion of the Waller Creek Watershed near the intersection of 24th St. and San Jacinto Blvd. on UT campus. The image on the left is composed of unfiltered LIDAR data; you can see trees covering the creek and buildings are intact. Images in the center and to the right show progressively more vegetation and building removal.

Figure 5. An all-points DEM and two versions of vegetation-removed DEMs showing how buildings are removed with vegetation.
The reason why buildings are removed along with vegetation is because the proprietary vegetation-removal algorithm we obtained with the purchase of the ALTM does not utilize first and last pulse data; it only uses last pulse data. As soon as we are able to develop a routine that utilizes first and last pulse data, we should be able to remove vegetation but keep buildings intact. For example, if a single pulse hits the top of a building, both the first and last pulse signals will reflect from the top of the building. If a single pulse hits a tree, a portion of the pulse will reflect from a leaf or branch and a portion will penetrate the tree and reflect from the ground. In this latter example, the first pulse will represent vegetation elevation and the last pulse will represent ground elevation.
Vegetation Removal and Hydrologic Modeling
In order to see the streambed in LIDAR images of vegetated areas, we must first remove the vegetation. An aspect of vegetation removal critical to hydrologic modeling is how well the cross section depicts streambed characteristics. For example, if we are removing the edges of buildings, are we also removing the edges of stream banks? And, how can we tell when we are removing vegetation completely? I looked for answers to these questions by extracting LIDAR data from the all-points and vegetation-removed data sets along a cross section of Waller Creek just south of the intersection of 24th St. and San Jacinto Blvd. This was done using a Fortran program that extracts points from a LIDAR data set 5m to either side of a cross section line defined by a series of x, y coordinates (Gutierrez, 2000). The location of the cross section is shown on the 1m DEM generated from the all-points data set (figure 6).
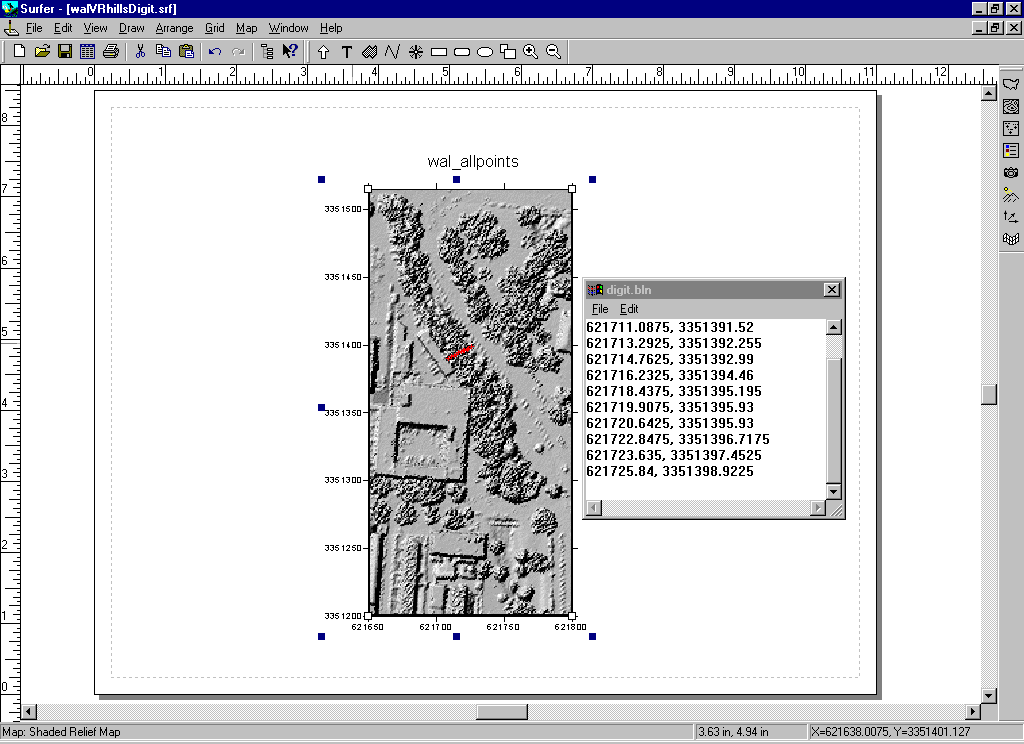
Figure 6. Location of LIDAR point cross sections.
Figures 7a, b, and c are plots of LIDAR data generated using the program Grapher.
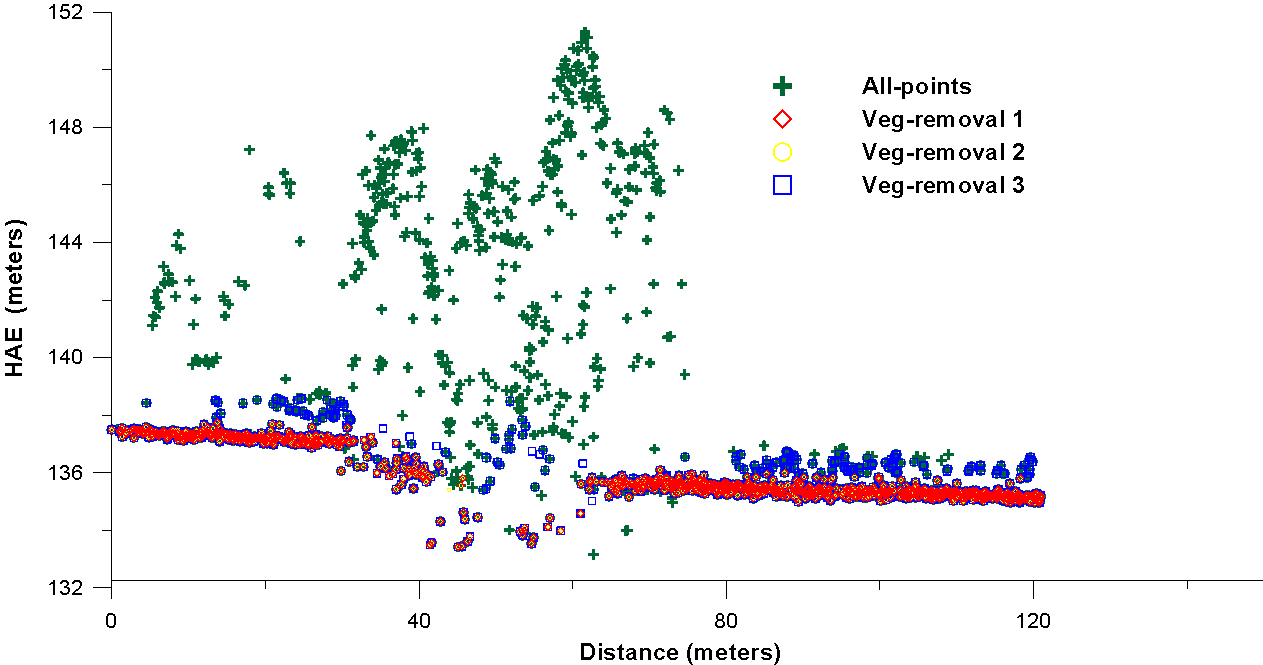
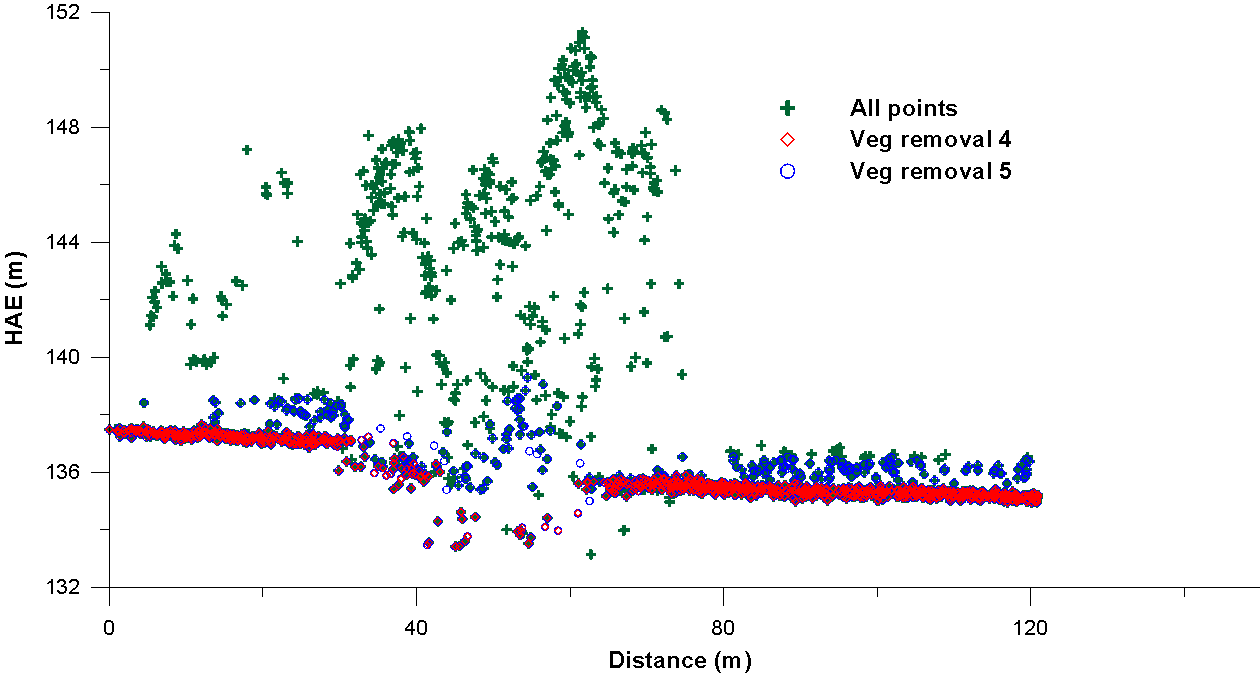
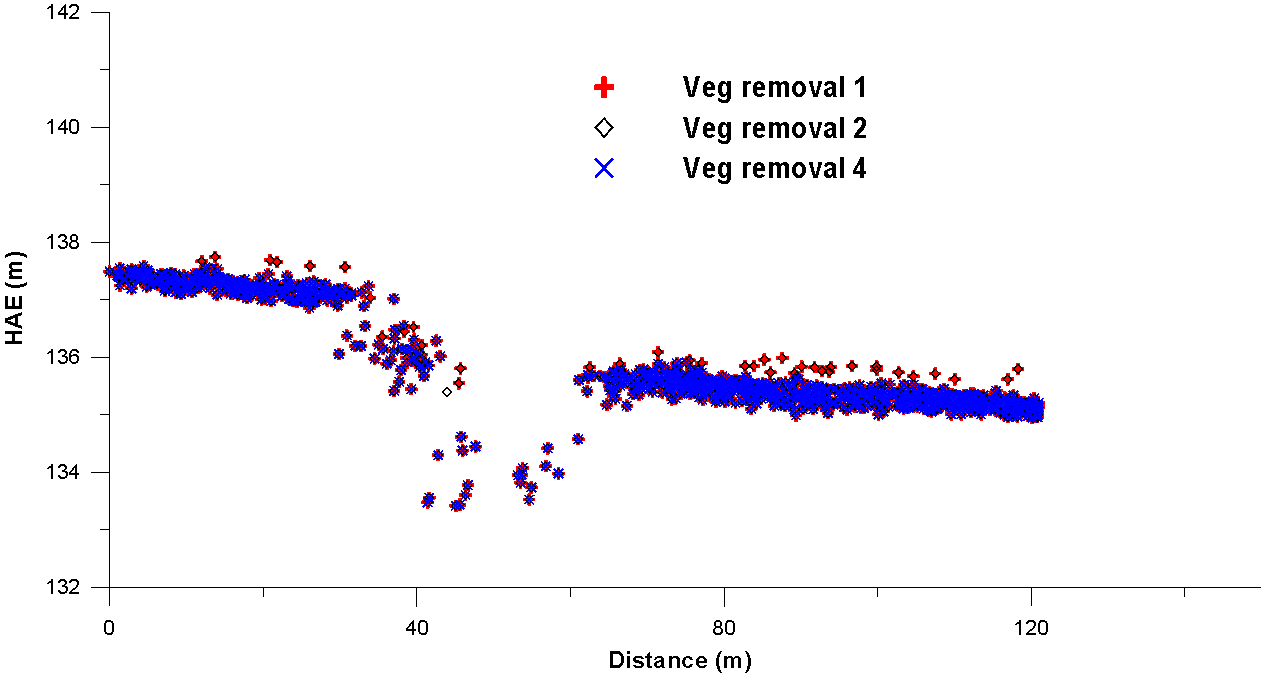
Figure 7. (a) Unfiltered (all-points) LIDAR data with results from vegetation-removal scenarios 1, 2, and 3. (b) Unfiltered (all-points) LIDAR data with results from vegetation-removal scenarios 4, and 5.
As seen in figure 7a, results of vegetation-removal scenarios 1 and 2 seem to best represent the ground surface. In figure 7b, results from scenario 4 seem to best represent ground surface. Figure 7c shows the best choices from 7a and 7b. While results from scenario 4 best represent the ground surface (i.e., 1 and 2 look like they may be indicative of low-lying bushes), it may also be excluding the edge of the stream bank on the west side (figure 7c). After inspecting the three plots in figure 7, I chose vegetation-removal scenario 4 as the best one to use for generating a vegetation-removed DEM of the Waller Creek Watershed.
Another question is: Can LIDAR-derived vegetation-removed DEMs more accurately represent streambed characteristics than TIN terrain models? In an attempt to answer this I compared a cross section extracted from the TIN using HEC-GeoRAS (figure 8) to one generated from LIDAR point data using vegetation removal scenario 4 settings (figure 9). Figures 8 and 9 show cross sections from approximately the same location on Waller Creek.
In order to compare the two data sets, I first had to adjust the LIDAR elevations from meters above the ellipsoid (HAE) to feet above mean sea level (AMSL). R. Gutierrez obtained from the GEOID99 model of North America a value of -25.815m for a coordinate corresponding to the center of the cross section across Waller Creek. GEOID99 is a model based on gravity measurements at the earthís surface that approximates the shape of the spheroid and itís divergence from an ideal ellipsoid. At the Waller Creek cross section, the shape of the earthís surface is approximately 26m below the reference ellipsoid as it is calculated using GPS (http://www.ngs.noaa.gov/GEOID/GEOID99).
After the orthometric height adjustment of the LIDAR data, the cross sections from the TIN (figure 8) and the LIDAR (figure 9) data sets match closely in elevation. Both figures show the west and east sides of the stream bank to be approximately 523 and 518ft AMSL, respectively. Figure 8 shows a more realistically shaped stream channel because it contains many more data points. I could do a more valid comparison of the two data sets if I used a cross section of a DEM of the vegetation-removed data set instead of the point data set, but I do not have one available at this time. However, if you imagine fitting a line to the points shown in
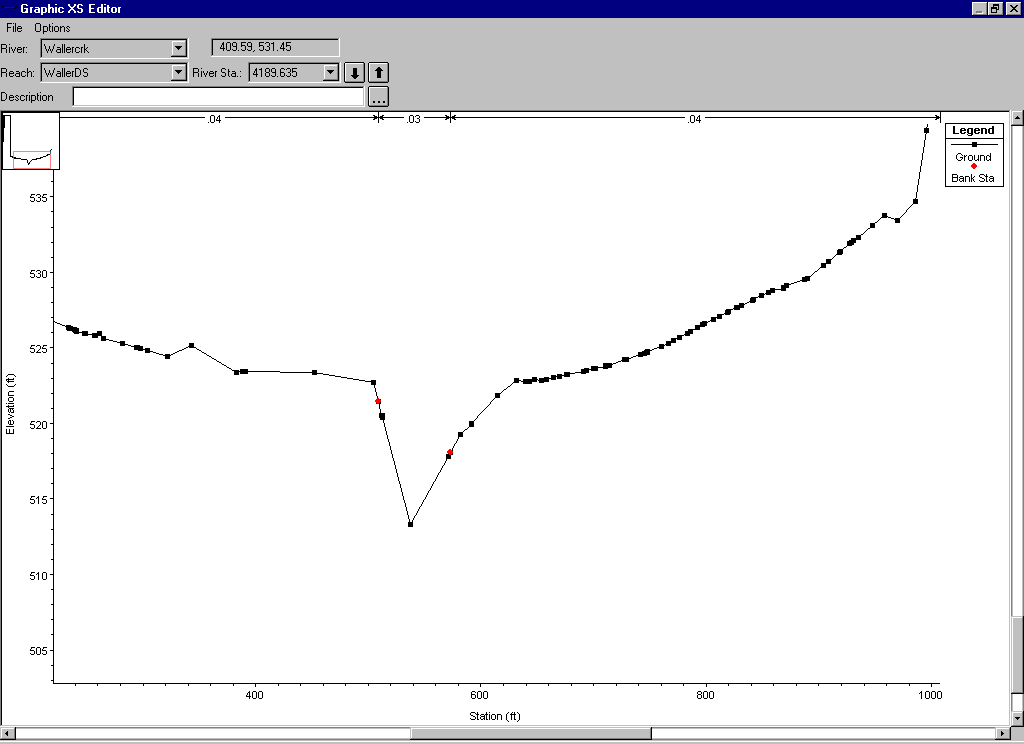
Figure 8. HEC-RAS Cross Section of Waller Creek Derived from TIN. Location is south of Bridge at 24th Street and San Jacinto Blvd. Note that the red dots show the edges of the channel.
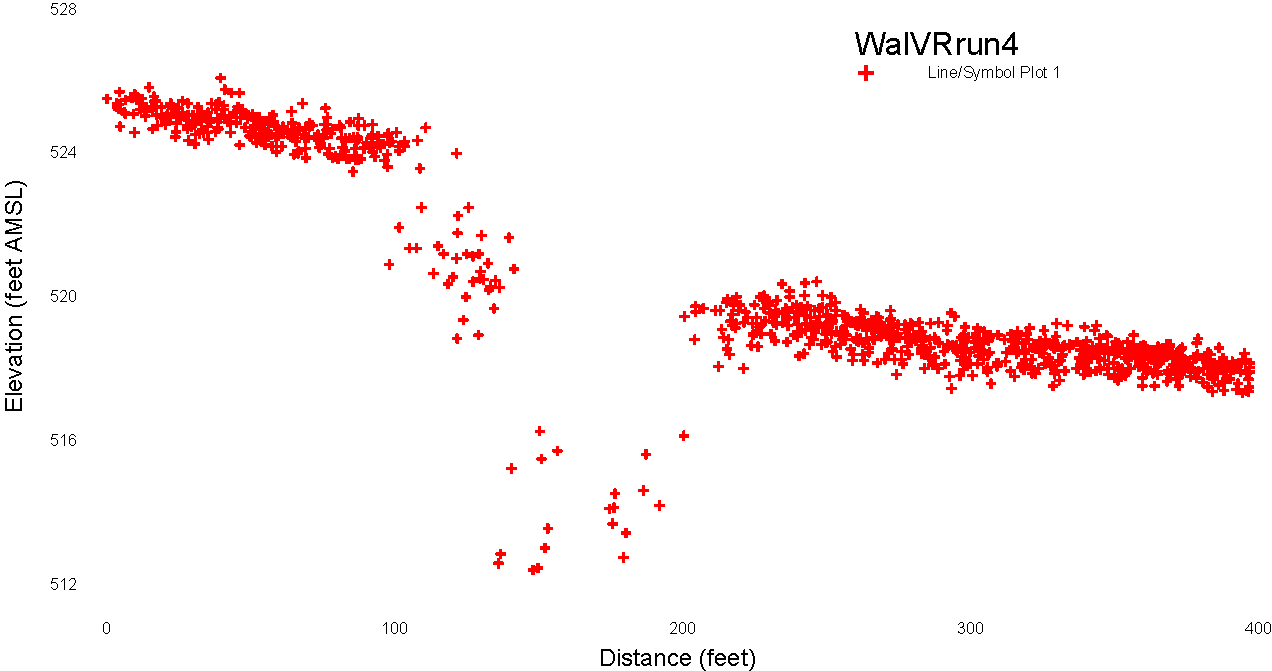
Figure 9. Grapher cross section of Waller Creek derived from LIDAR DEM (created in Surfer). Location is south of Bridge at 24th Street and San Jacinto Blvd.
figure 8, you can see that a DEM of the LIDAR data will more accurately depict the shape of the stream bed than the TIN.
CONCLUSIONS
The Snead and Maidment (2000) exercise and supplemental reading from the HEC-RAS manual have provided me with a very good introduction to HEC-RAS and HEC-GeoRAS. My original (or at least original revised) plan for the term project was to complete the CE class exercise using the provided TIN. I had then planned to repeat the exercise using a TIN generated from LIDAR data.
After generating five sets of vegetation-filtered data for Waller Creek using a proprietary algorithm included with the purchase of the ALTM, I chose one that best removes vegetation. At this time, I have a Bare-Earth Digital Elevation Model (DEM) of the area of interest, but have not yet adjusted the entire grid to orthometric heights nor have I generated a TIN from those data. It will likely take me until the end of Summer 2001 before I am able to finish a hydrologic modeling exercise using LIDAR data.
Channel cross sections extracted from a TIN terrain model using HEC-GeoRAS can contain up to 500 elevation points. A similar channel cross section through a set of LIDAR data may contain at least 1000 elevation points. We can more accurately depict the stream channel in cross section using the LIDAR data, but the large number of data points will overwhelm any hydrologic modeling program.
REFERENCES
Gutierrez, Roberto, 2000, library of Fortran programs written to manipulate LIDAR point datasets.
HEC-RAS 2.2 software manual.
Snead, Daniel and Maidment, D. R., 2000, Floodplain Visualization Using HEC Geo-RAS: University of Texas at Austin Civil Engineering class exercise, 39p.