The intention of this exercise is to give you experience applying Arcview to view maps in various commonly used projections, and to introduce you to a few more functions within the Arcview interface, such as the procedure for selecting a class of features for display in a map. In this exercise you will also learn how to convert Arcview Shapefiles into Arc/Info coverages, how to make a projection file and use it in Arc/Info to do map projections.
The data needed for this exercise are contained in the /avdata sample data sets that are distributed by ESRI along with the code for Arcview. In particular, this exercise uses data from the /qstart, /namerica and /world subdirectories of the /avdata sample data set which is located on the LRC server at civil/class/maidment/ce397/avdata.
The data can also be downloaded via via anonymous ftp from ftp.crwr.utexas.edu/pub/gisclass/ex3. You will need Arcview shape files for the data layers named cnty, deg30, latlong, states, and world94. Each of these shape files has several component files whose extensions are .dbf, .shp, .shx, etc. You will need ALL of these files in order to view the shape file in ArcView. If you are using ftp from the command line, you can use the command mget filename.* to get all files whose stem name is filename. Ftp will prompt you for each file and ask if you want to transfer the file. Use the Binary option of ftp for these file transfers. If necessary, see Instructions on how to use anonymous ftp.
The part of the exercise concerned with viewing map projections is done with Arcview 2 or Arcview3 on either a workstation, PC or MacIntosh platform. The later part dealing with using map projections to produce new data sets must be done with Arc/Info.
(1) Prepare a set of three layouts showing how the world, the United States and Texas look in geographic coordinates and in various map projections
(2) Answer other questions about the analysis that you perform as noted on the instructions in the following pages.
Turn in these answers along with your map and give a brief comment on any difficulties that you had with this exercise.
Map projection involves taking data whose spatial coordinates are defined in terms of latitude and longitude on a curved earth surface and transforming those data so that their spatial coordinates are defined in terms of Easting and Northing or (x,y) on a flat map surface. ArcView permits data to be viewed in various map projections but no new data sets are produced in these projections. Arc/Info permits transformation of data into new projected coordinate systems but use of Arc/Info for this purpose is not included in this exercise.
To begin this exercise, you need to be working at a PC machine with Arcview 2.1 or 3.0 operating and have access to the sample data files which are stored in the same directory as Arcview.
Start Arcview and open a new View. Add themes World94.shp, and Deg30.shp. Drag Deg30.shp below the World94.shp so that the layout of the countries is superimposed on the grid of 30 degree rectangles. Recolor the countries and 30 degree rectangles as necessary. If you want to make the Deg30 rectangles clear and show just their outlines, highlight this theme in the tool palette, click on the Legend symbol, and in the Legend Editor window that opens, click on this symbol again. In the Fill Palette window that then opens, click on the clear rectangle in the top left corner of the shaded rectangles displayed, then select Apply in the Legend Tool window and the display of the Degree boxes will go to outlines only.
Here is an view of the World in Geographic Coordinates
Move the cursor around on the view and you will see a pair of numbers above the view on the toolbar to the right of "scale" that alter as you move the cursor. These give the location of the cursor and from the values displayed you can see that these data are displayed in Decimal Degrees of Latitude and Longitude.
To be turned in: what is the spatial extent of the view shown in terms of degrees of latitude and longitude? Where is the point (0,0) latitude and longitude located on the earth's surface?
Make a new View by hitting New in the Project window while the View icon is highlighted. This should result in the creation of a new View window labeled View2. Add the themes World94.shp and Deg30.shp as before.
Click on "View/Properties" and you will see a window open with options for Projection. Click on the "Projection" button. Under "Projections of the World" you'll see a projection "Type" labeled "Robinson". Click Ok in the two open windows and you'll see the View transformed to appear in a Robinson projection, which is a relatively new style of map projection for the earth designed to present the whole earth with a minimum of distortion at any location. If you move the cursor over this space, you'll see that the coordinates are now in a very different set of units, meters in the projected coordinate system.
Go back to "View/Properties" and under Projection "Type", click on the arrow to the right of "Robinson", which opens a display window, from which you can select "Geographic". Click, ok, ok, and the View will be transformed back to the appearance that it had originally.
Go back to View/Properties and reproject the View into the Robinson projection.
Here is an example view of the World in Robinson Projection
Create another new View (View 3) by the same procedure as used previously, added World94.shp and Deg30.shp as themes to it.
Go to the View/Properties sequence and this time under projection Type, select "View from Space" (the last option in the list of "Projections of the World"). You'll see a nice 3-D view of the globe as seen from a viewpoint above Massachusetts. If you want to see how the world looks when viewed from above Austin, Texas, go back to the projection selection window, click on "Custom" and then type -97 for the Central Meridian and 31 for the reference latitude. And there is the world centered on Austin, Texas! You may wish to try looking at the world from a few other places. You can get the coordinates of locations on the earth by viewing earth in the geographic projection. Play around a bit and have some fun!
Here is an example view of the World from Space above Austin, Texas
The Project should now contain three Views of the world: in Geographic
coordinates, the Robinson Projection and the View from Space. Make sure
that they are all open. In the Project Window, click on the Layout icon
and hit New. This will create a blank layout window. Use the map icon ![]() at the right end of the lower tool bar to create a space on the layout
for View 1 and add the View to this space. Repeat the Exercise for View2
and View3.
at the right end of the lower tool bar to create a space on the layout
for View 1 and add the View to this space. Repeat the Exercise for View2
and View3.
Label the Views of the World with the Character Tool ![]() in the lower tool bar. If your labeling is too small (the default is 14
point), use Window/ Show Symbol Palette to bring up the Palette, click
on the button labeled ABC to get the Font Palette and then resize the lettering
to perhaps 24 or 36 point. If you want to color the lettering, choose the
Paintbrush icon in the Tool Palette, and in the Color
Palette, scroll forward from Foreground to Text, then choose the color
for the text. Label some of the main meridians and parallels in the geographic
coordinate view.
in the lower tool bar. If your labeling is too small (the default is 14
point), use Window/ Show Symbol Palette to bring up the Palette, click
on the button labeled ABC to get the Font Palette and then resize the lettering
to perhaps 24 or 36 point. If you want to color the lettering, choose the
Paintbrush icon in the Tool Palette, and in the Color
Palette, scroll forward from Foreground to Text, then choose the color
for the text. Label some of the main meridians and parallels in the geographic
coordinate view.
Make a printout of the Layout. Save the Project (File/Save Project As) so that you don't have to recreate it again later if you need it again.
Here is an example of the Layout of Projections of the World
To be turned in: A printout of the Layout showing the three views of the world
In this part of the exercise, we are going to examine map projections used for the continental United States.
Create a New Project by hitting File/New Project. Save changes
to your previous project if necessary before it is automatically closed
out. Open a new View. Add themes to the States.shp and latlong.shp.
These are an outline of the United States and a 5 degree grid of latitude
and longitude as a line theme. Position the latlong theme above the States
theme so that you can see the grid overlying the country. Zoom in so that
you have a view just of the continental United States, not including Alaska.
Use the little hand tool ![]() to drag
the United States into the center of the view window if necessary. Pretty
cool!
to drag
the United States into the center of the view window if necessary. Pretty
cool!
Here is an example of the United States in Geographic Coordinates
Question: What is the geographic extent of the United States? Give the East and West limits of longitude of the continental US and those for the Northern and Southern extent of the continent to the nearest degree. Which parallel defines much of the border between the United States and Canada? If we removed a vertical slice out of the world cut along the meridians defining the most Eastern and Western points in the continental United States, how much of the globe would we have cut out?
The Albers Equal Area projection has the property that the area bounded by any pair of parallels and meridians is exactly reproduced between the image of those parallels and meridians in the projected domain, that is, the projection preserves the correct area of the earth though distorts direction, distance and shape somewhat.
Create a new View, View2, and add Latlong and States.shp to the View as you did previously. Go to View/Properties and ensure that Map Units are labeled Decimal Degrees since the View that you are looking at is in Geographic Coordinates. Hit Projection, select Projections of the United States, and among the choices offered, select the Albers Equal-Area Conic projection.
Make a note of the Ellipsoid used and the projection parameters (Central Meridian, Reference Latitude, Standard Parallel 1, Standard Parallel 2, False Easting and False Northing).
Here is an example of the Albers Equal Area Projection of the United States
Separate View1 (Geographic Coordinates) and View2 (Albers Projection) and you will see that in geographic coordinates the United States appears to be wider and flatter than it does in normal projected coordinates. This does not occur because Canada is sitting on the USA and squishing us! This effect occurs because as you go northward, the meridians converge toward one another while the successive parallels remain parallel to one another. When you reach the north pole, the meridians converge completely.
If you take a 5 degree box of latitude and longitude, such as one of those shown in the views, the ratio of the East-West distance between meridians to the North-South distance between parallels is Cos (latitude) : 1. For example, at 30°N, Cos(30°) = 0.866, so the ratio is 0.866 : 1, at 45°N, Cos(45°) = 0.707, so the ratio is 0.707 : 1. In the projected Albers view (View2), the result is that square boxes of latitude - longitude appear as elongated quadrilaterals with a longer base than their top edge. In geographic coordinates, the effect of the real convergence of the meridians is lost because the latitude and longitude grid form a set of perpendicular lines, which is what makes the United States seem wider and flatter in geographic coordinates than it does in the more normal projected map coordinates.
The Project should now contain two Views of the United States: in Geographic coordinates, and in the Albers Equal Area projection. Make sure that they are all open. In the Project Window, click on the Layout icon and hit New. This will create a blank layout window. Use the map icon at the right end of the lower tool bar to create a space on the layout for View 1 and add the View to this space. Repeat the Exercise for View2.
Label the Views of the United States with the Character Tool . If your labeling is too small (the default is 14 point), use Window/ Show Symbol Palette to bring up the Palette, click on the button labeled ABC to get the Font Palette and then resize the lettering to perhaps 24 or 36 point. Label some of the main meridians and parallels in the geographic coordinate view.
Here is an example of the Layout of Projections of the United States
Make a printout of the Layout. Save the Project (File/Save Project As) so that you don't have to recreate it again later if you need it again.
To be turned in: A printout of the Layout showing the two views of the United States
In this portion of the exercise, we are going to look at the State of Texas and the effect of various map projections upon a map of the State.
Make a new project, open a View and add to the View the themes Cnty and Latlong.. The theme Cnty is a counties coverage of the United States. When you click on the themes to open them, you will see that the coverage is over all the United States, including Alaska and Hawaii.
To select the counties which make up Texas, a special display of the counties theme can be set up as follows:
Questions: What is the geographic extent of Texas to the nearest degree in North, South, East and West? What meridian runs down the East side of the Texas Panhandle?
The Lambert Conformal Conic projection is a standard projection for presenting maps of land areas whose East-West extent is large compared with their North-South extent. This projection is "conformal" in the sense that lines of latitude and longitude, which are perpendicular to one another on the earth's surface, are also perpendicular to one another in the projected domain.
Create a new View (View2), add Latlong and Cnty to it, and select the counties in Texas as before.
To view Texas in the Lambert Conformal Conic projection, highlight the Cnty theme, go to View/Properties, set the map units to Decimal Degrees, click on the Projection bar and in the Projection Properties window displayed, select Category: Projections of the United States, and Type: Lambert Conformal Conic (Conterminous U.S.). Click OK to the two display windows to transform the view to the projected domain. Notice how the meridians now fan out from an origin at the center of rotation of the earth (a consequence of using a conic projection centered on the axis of rotation of the earth). The display shown is that which would be produced by cutting the cone up the back side and unfolding the cone so that it lays flat on the table.
Here is an example of the Lambert Conformal Conic Meridians and Parallels
Texas is a dark dot in the center of the meridians. Use the Zoom tool to highlight the State. Notice that Texas appears to be tilted to the right slightly. This occurs because the Central Meridian of the projection use is 96W, which would appear as a vertical line in the display. Regions to the West of this meridian (most of Texas) appear tilted to the right while those to the East of this meridian appear tilted to the left.
In order to present a pleasing map of Texas, and to minimize distortion of distance in State-wide maps, the Texas State GIS Committee, has approved a standard projection of Texas called the Texas State Mapping System. The definition of this projection is:
Datum: North American Datum of 1983 (NAD83)
Ellipsoid: Geodetic Reference System of 1980 (GRS80)
Map units: meters
Central Meridian: 100°W (-100.0000)
Reference Latitude: 31° 10´ N (31.166667)
Standard Parallel 1: 27° 25´ N (27.416667)
Standard Parallel 2: 34° 55´ N (34.916667)
False Easting: 1000000
False Northing: 1000000
This means the standard parallels where the cone cuts the earth's surface are located at about 1/6 of the distance from the top and bottom of the State, respectively, and that the origin of the coordinate system (at the intersection of the Central Meridian and the Reference Latitude) is in the center of the State, to which the coordinates (x,y) = (1000000, 1000000) meters is assigned so that the (x,y) coordinates of all locations in the State will be positive.
To transform the projection to Texas State Mapping System coordinates, highlight View2, to again to View/Properties, hit Projection and in Projection Properties, click Custom at the top of the form. You will see that the Ellipsoid now has ascroll bar, choose GRS 80; and type the parameters given above into the boxes beside each of the parameters in the form. Hit OK, OK, and Presto! you'll see the map of Texas transformed to a nice upright appearance!
Here is an example of the Texas State Mapping System Projection
Questions: What are the approximate width and length in km of Texas
at its widest and longest points? What are the coordinates of El Paso,
the farthest point in the West of Texas, in this coordinate system? What
are the coordinates in this system of Brownsville, the most southern city
in Texas? (Hint: Use the measuring tool![]() in the lower tool bar of the View window to measure distance across Texas).
in the lower tool bar of the View window to measure distance across Texas).
The Universal Transverse Mercator projection is actually a family of projections, each having in common the fact that they are Transverse Mercator projections produced by folding a horizontal cylinder around the earth. The term transverse arises from the fact that the axis of the cylinder is perpendicular or transverse to the axis of rotation of the earth. In the Universal Transverse Mercator coordinate system, the earth is divided into 60 zones, each 6° of longitude in width, and the Transverse Mercator projection is applied to each zone along its centerline, that is, the cylinder touches the earth's surface along the midline of each zone so that no point in a given zone is more than 3° from the location where earth distance is truly preserved.
Create a new View, View3, in the Project and add Cnty and Latlong to the theme in the same manner as previously, selecting the counties of Texas using the Theme Properties window. Project the View into Universal Transverse Mercator projection by using View Properties/Projection Properties, under Category: select UTM, and under Type, select Zone 14. You will see a standard set of projection parameters displayed which include:
Projection: Transverse Mercator
Ellipsoid: GRS 80
Central Meridian: -99.00000
Reference Latitude: 0.00000
Scale Factor: 0.99960
False Easting: 500000
False Northing: 0.00000
These parameters mean that the Central Meridian of Zone 14 is at 99°W so that it covers from 96°W to 102°W; the Reference Latitude is 0.0000 (the equator, which is 0°N); the origin of the coordinate system is at the intersection of the Central Meridion with the Reference Latitude and thus is at (0°N, 99°W), where the coordinates are (x, y) = (500,000, 0) m. The false Easting of 500,000m is to ensure that all points in the zone have positive x coordinates. The y-coordinates are always positive in the Northern hemisphere because 0 is at the equator. In the Southern Hemisphere, a false Northing of 10,000,000m is applied to ensure that the y-coordinate is always positive.
The Scale Factor of 0.9996 means that along the Central Meridian, the true scale of 1.0 is reduced slightly so that at locations off the true meridian the scale factor will be more nearly 1.0 (the Transverse Mercator projection distorts distance positively as you move away from the Central Meridian).
Click, OK, OK, to see the projection applied. The pattern of meridians and parallels looks strange, converging at top and bottom of the picture, which correspond to the North and South Poles, respectively. When you zoom in on Texas, the map of the State looks much as it did in the Texas State Mapping System using the Lambert Conformal Conic projection.
Here is an example of the Texas in the UTM Projection, Zone 14
Questions: How many UTM zones does it take to cover Texas? Which zone applies in West Texas? Central Texas? East Texas?
The Project should now contain three Views of the Texas: in Geographic coordinates, the Texas State Mapping System and the Universal Transverse Mercator projection. Make sure that they are all open. In the Project Window, click on the Layout icon and hit New. This will create a blank layout window. Use the map icon at the right end of the lower tool bar to create a space on the layout for View 1 and add the View to this space. Repeat the Exercise for View2 and View3.
Label the Views of Texas with the Character Tool (Labeled T in the lower tool bar). If your labeling is too small (the default is 14 point), use Window/ Show Symbol Palette to bring up the Palette, click on the button labeled ABC to get the Font Palette and then resize the lettering to perhaps 24 or 36 point. Label some of the main meridians and parallels in the geographic coordinate view.
Here is an example of the Layout of Projections of Texas
Make a printout of the Layout. Save the Project (File/Save Project As) so that you don't have to recreate it again later if you need it again.
To be turned in: A Layout showing Texas in geographic coordinates and in the two map projections.
The spatial transformations that you have been doing up to now in Arcview have been for viewing purposes only. The original spatial data were unaltered by these actions. Lets go a step further now and actually transform the spatial data to the new coordinate system. The present version of Arcview cannot perform this transformation so we must use Arc/Info instead. If necessary, quit the machine you are working on and log on to one that runs Arc/Info. We are going to use the county theme of the United States cnty as an example. If necessary, ftp the files cnty.shp, cnty.shx, cnty.dbf from the anonymous ftp site into your working directory.
These files are called Arcview Shapefiles, a special data format that was created for Arcview and which is not readily handled by Arc/Info. First we must transform these files into an Arc/Info coverage. Start up Arc/Info and type: Arc: shapearc cnty county
The shapearc creates an arc coverage called county, including an attached attribute file in the Info directory from the cnty shape files (the reverse action can be accomplished by the arcshape command). We now need to reconstruct the polygons that make up each county from the arcs along their borders. First, we have to clean the arc coverage so that nodes are created where arcs cross one another. The use of # in a command indicates that the default value of a parameter should be used. In this case, we'll use the default dangle length and fuzzy tolerance, which are parameters defining the way points and lines are manipulated when they are close together.
Arc: clean county county1 # # poly
Cleaning /HOME1/ALPHA62/MAIDMENT/EX3/COUNTY
Sorting...
Intersecting...
Assembling polygons...
Re-building AAT...
Now we'll build the polygons and the polygon attribute table:
Arc: build county1 poly
Building polygons...
Re-building AAT...
Lets check out whether we've got a polygon attribute table:
Arc: items county1.pat
COLUMN ITEM NAME WIDTH OUTPUT TYPE N.DEC ALTERNATE NAME
1 AREA 4 12 F 3 -
5 PERIMETER 4 12 F 3 -
9 COUNTY1# 4 5 B - -
13 COUNTY1-ID 4 5 B - -
Ok, everything looks good. Now lets do the map projection.
The original cnty shape files were in units of decimal degrees. That
can be verified by displaying them in Arcview, moving the cursor over the
view, and looking at the coordinates displayed to the upper right of the
view. You'll see numbers like ![]() which means that the point at which the cursor is now located is at 122.05
degrees West and 43.20 degrees North. When expressed numerically, West
longitudes by convention are negative while East longitudes are positive.
Likewise, North latitudes are positive and South latitudes are negative.
The number 43.20 is a latitude expressed in decimal degrees.
which means that the point at which the cursor is now located is at 122.05
degrees West and 43.20 degrees North. When expressed numerically, West
longitudes by convention are negative while East longitudes are positive.
Likewise, North latitudes are positive and South latitudes are negative.
The number 43.20 is a latitude expressed in decimal degrees.
To do projections in Arc/Info you use the Project command whose parameters can be specified by a dialog, but it is more convenient to type out a text file with all the responses that would be needed in the dialog and input that at the time the project command is initiated.
The format for a projection file is the following:
input
projection
units
datum
parameters
output
projection
units
datum
parameters
end
You'll see that this file has a section for the input and for the output. Each section contains:
Notice that the projection file always has end as its last line. Doing map projections is a complex process and you can make use of the HELP system in Arc/Info to determine what values are appropriate for each part of the projection file. For the moment, we'll create a simple projection file which transforms the data from geographic coordinates in decimal degrees to an Albers Equal Area projection of the United States with standard parameters appropriate for viewing maps of the continental US. Open a text editor and type in the following (make sure that you hit return after typing end). Save the file as albers.prj.
input projection geographic units dd datum NAD83 parameters output projection albers units meters datum NAD83 parameters 29 30 0.000 45 30 0.000 -96 0 0.000 23 0 0.000 0.00000 0.00000 end
This file assumes that the input coverage is in geographic coordinates with units of decimal degrees (dd) using the NAD83 datum. The command parameters is included in the input section but no parameters follow it because none are needed to further describe the input data projection. The output coordinate system is an Albers Equal Area projection with horizontal distance units in meters, defined assuming the NAD83 datum, with standard parallels at 29 degrees 30 minutes and 45 degress 30 minutes North, a central meridian at 96 degrees West, a reference latitude of 23 degrees North, and zero Xshift and Yshift, which means that a point at (96W, 23N) degrees will become (0,0) meters in the projected Albers coordinate system.
Now lets do the map projection using the county1 coverage that was created earlier. We'll call the projected coverage county2:
Arc: project cover county1 county2 albers.prj
Once the new arc coverage has been created, the polygons need to be rebuilt in the projected coordinate system:
Arc: build county2 poly
Building polygons...
Re-building AAT...

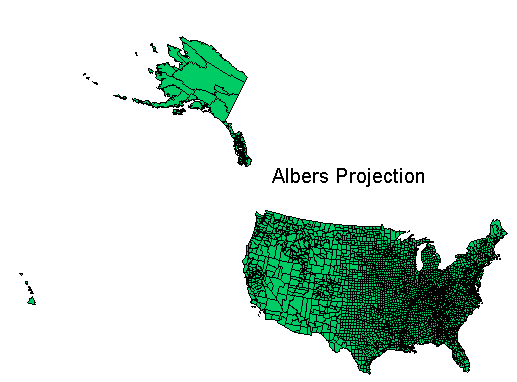
You can see that while these projection parameters produce a reasonable map for the continental United States, they are not suitable for Alaska or Hawaii.
Now lets use the describe command to see what coordinate system we have.
Arc: describe county1
Arc: describe county2
The output from this command is initially a set of details about the spatial data. Scroll down and you'll come to the part about the Coordinate System Description. In the case of county1 you should find that no coordinate system has been defined (the data are in decimal degrees and the coverage doesn't contain a prj file). For county2, you'll find that the details of the Albers coordinate system are presented.
To be turned in: a copy of the textfile you used for the map projection and the Coordinate System Description of the input and output coverages used in the map projection.
Click here to get additional information about projections, including datum conversions, azimuthal projections, and some complete files for projection from one coordinate system to another.
Click here to see an example for the parameters for Geographic-WGS72
Click here to see an example for the parameters for Geographic- WGS84
Click here to see an example for the parameters for US Albers Equal Area
Click here to see an example for the parameters for TSMS Lambert Conformal Conic
Click here to see an example for the parameters for TSMS Albers Equal Area
You can create a folder in your account where you can maintain a small library of projection files so that you can get from one coordinate system to another without having to make up a file from scratch every time.
Now that you have some experience with presenting maps in Arcview with various map projections, I'd like you to dig around in the /avdata (located on the LRC PC server at civil/class/maidment/ce397/avdata), or elsewhere, and develop a new map or Layout of something of interest to you in an appropriate map projection. Some suggestions:
To be turned in: a Layout showing the map in geographic coordinates and in coordinates of the chosen projection
Feel free to be creative and expand on what I've suggested in the direction of your own interests. Another one done!!